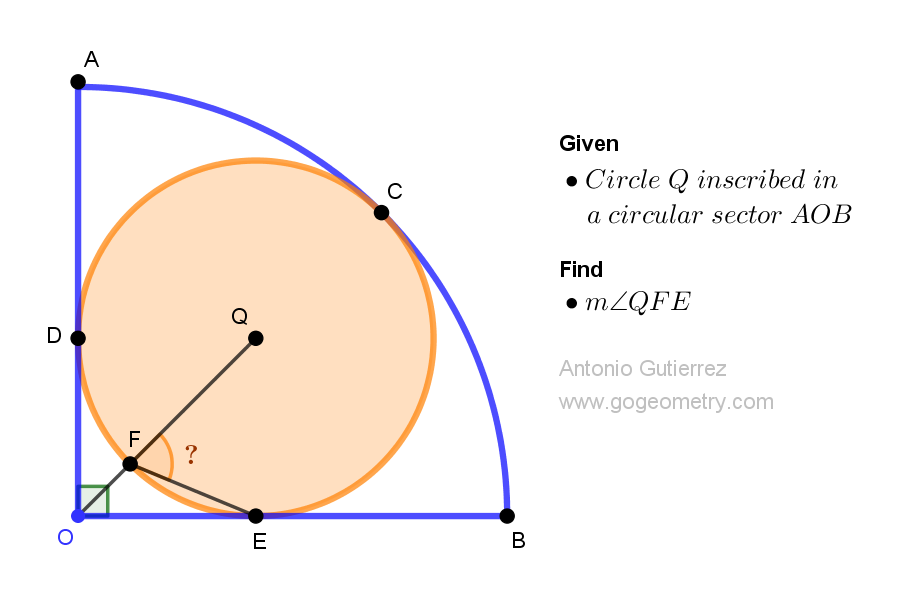
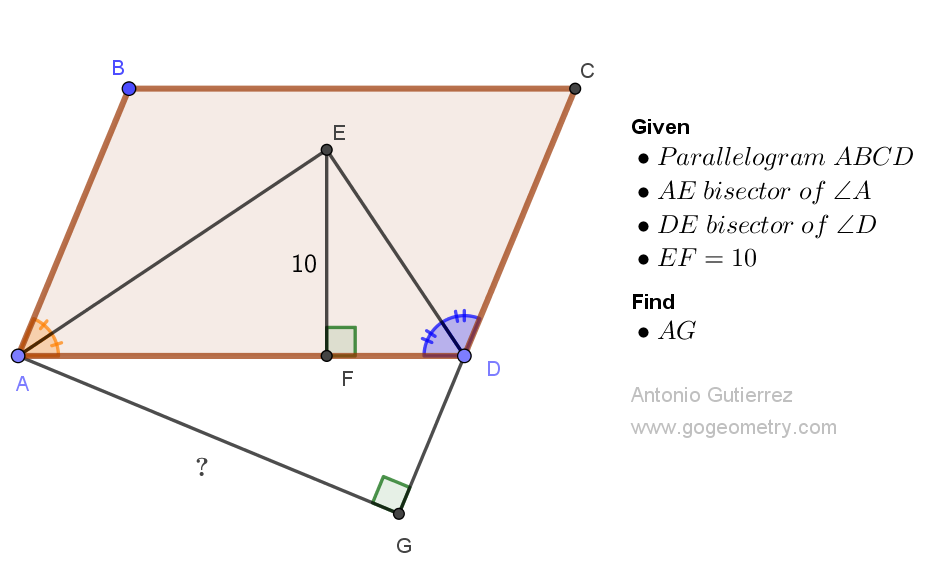
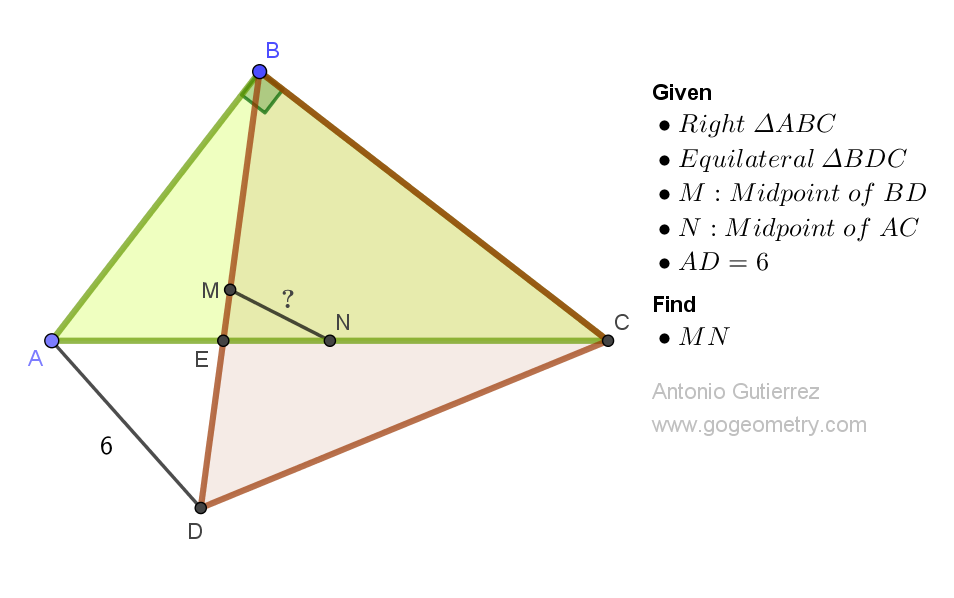
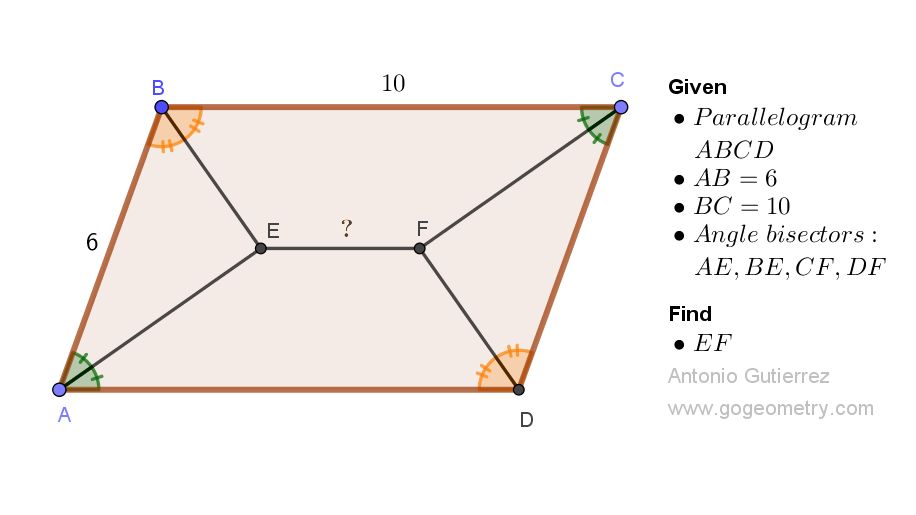
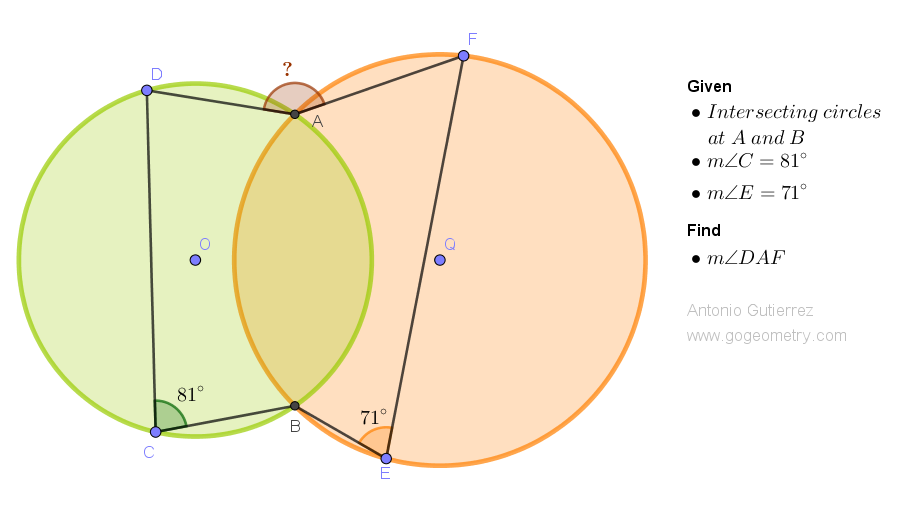
Geometry Problem 1527: Discovering the Hidden Angle: Solving the Puzzle of Two Intersecting Circles. Difficulty Level: High School.

Consider two circles with centers O and Q that intersect at points A and B. In circle O, draw a chord BC, and take point D on arc AC such that angle BCD measures 81 degrees. Similarly, in circle Q, draw a chord BE, and take point F on arc AE such that angle BEF measures 71 degrees. Find the measure of angle DAF.

Geometry Problem 1527: Discovering the Hidden Angle: Solving the Puzzle of Two Intersecting Circles

View or post a solution

Geometry Tips Now!

Element Definition Theorem/Comment
Circle A closed curve where every point on the curve is equidistant from the center point The diameter of a circle is the longest chord of the circle
Intersecting Circles Circles that have one or more points in common The common chord of two intersecting circles is the perpendicular bisector of the line joining the centers of the circles
Chord A line segment that connects two points on a circle The perpendicular bisector of a chord passes through the center of the circle
Common Chord A chord that is common to two or more circles  
Inscribed Angle An angle whose vertex is on the circumference of a circle and whose sides pass through two other points on the circumference An inscribed angle is half of the measure of the arc that it intercepts
Cyclic Quadrilateral A quadrilateral whose vertices lie on a circle The opposite angles of a cyclic quadrilateral are supplementary
 

Discover Even More: See Also...

Problem 1528

Geometry Problem 1528: Cracking the Circle Code: Unveiling the Tangent and Angle of an Inscribed Circle within a 90-Degree Circular Sector

Problem 1526

Geometry Problem 1526: Mastering Geometry Problem-Solving: Discover the Distance Between Two Sides in a Parallelogram Using Bisectors and Distance Measures

Problem 1525

Geometry Problem 1525: Unveiling the Secrets of Equilateral Triangles in Right Triangle Geometry: Finding the Midpoint Distance between Segments

Problem 1524

Geometry Problem 1524: Unlock the Mystery of Parallelograms: Discover the Length of Segment between the Intersecting Angle Bisectors

Problem 1523

Geometry Problem 1523: Discover How to Calculate the Length of the Altitude in an Isosceles Triangle - Get Expert Geometry Tips Now!

Problem 1522

Geometry Problem 1521: UUnlocking the Angle Measure of a Triangle with Median and Doubled Side Lengths. Difficulty Level: High School.

Thematic Poem:
Discovering the Hidden Angles of Circles through Chords

Amidst the circles' intersecting lines,
A puzzle awaits the curious mind,
For hidden angles to seek and find,
A challenge that tests our mathematical fines.

With chords as clues, we start the quest,
To solve the puzzle with our very best,
And unlock the secrets of the circles' crest,
For knowledge and wisdom to manifest.

We delve into the realm of geometry,
And discover the wonders of symmetry,
As we unravel the puzzle's mystery,
With the angles revealed in their majesty.

The hidden angle, a treasure to behold,
A reward for the persistent and bold,
As we witness the beauty of math unfold,
And our minds expand with the knowledge we hold.

So let us continue the pursuit,
Of discovering the hidden angles en route,
And solving the puzzle with resolute,
For the joys of learning to compute.

If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.

Recent Additions

Geometry Problems
Open Problems
Visual Index
All Problems
Circle
Intersecting Circles
Common Chord
Chords
Cyclic Quadrilateral
View or Post a solution 

Search our site with Google: