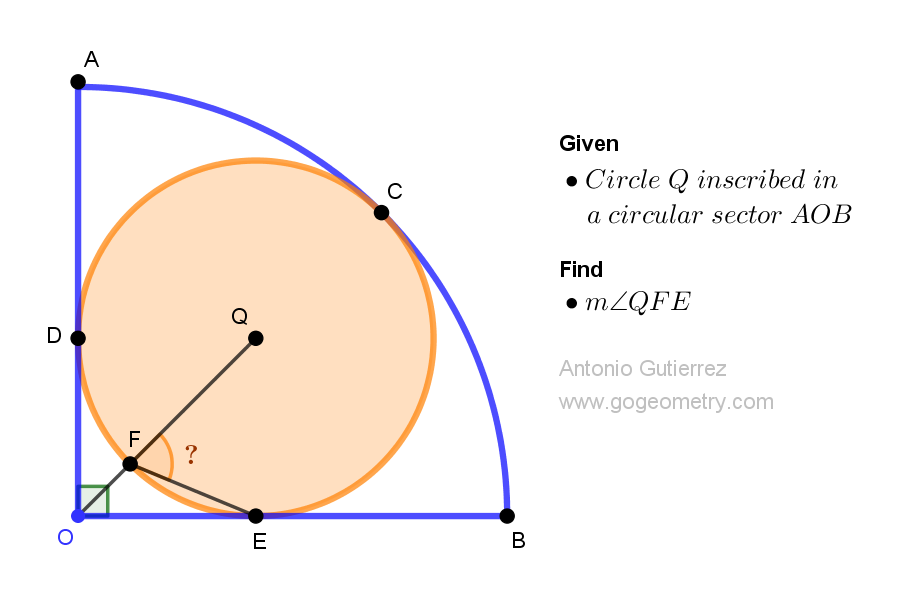
Geometry Problem 1528: Cracking the Circle Code: Unveiling the Tangent and Angle of an Inscribed Circle within a 90-Degree Circular Sector. Difficulty Level: High School.

Thematic Poem:
Unlocking the Circle's Hidden Code

Within a circle's bounds we seek,
To find the hidden code unique.
A tangent and an angle rare,
Within a sector, we'll find them there.

With careful measure and calculation,
We'll unlock this circle's foundation.
For in its inscribed form we see,
A world of geometry.

The tangent line, it touches close,
A point of contact we disclose.
And from that point, we measure true,
The angle that we seek anew.

Within this ninety-degree space,
We find the circle's hidden grace.
Its tangents and angles now revealed,
A treasure trove that's unconcealed.