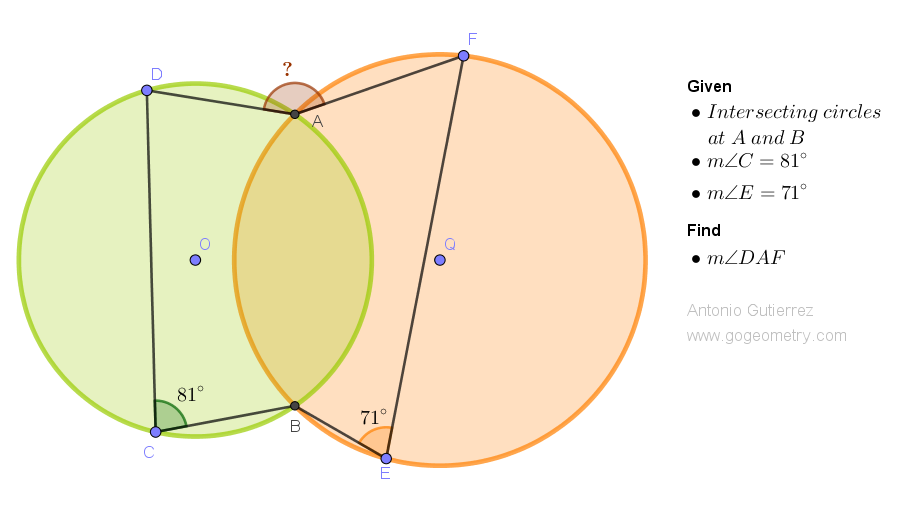
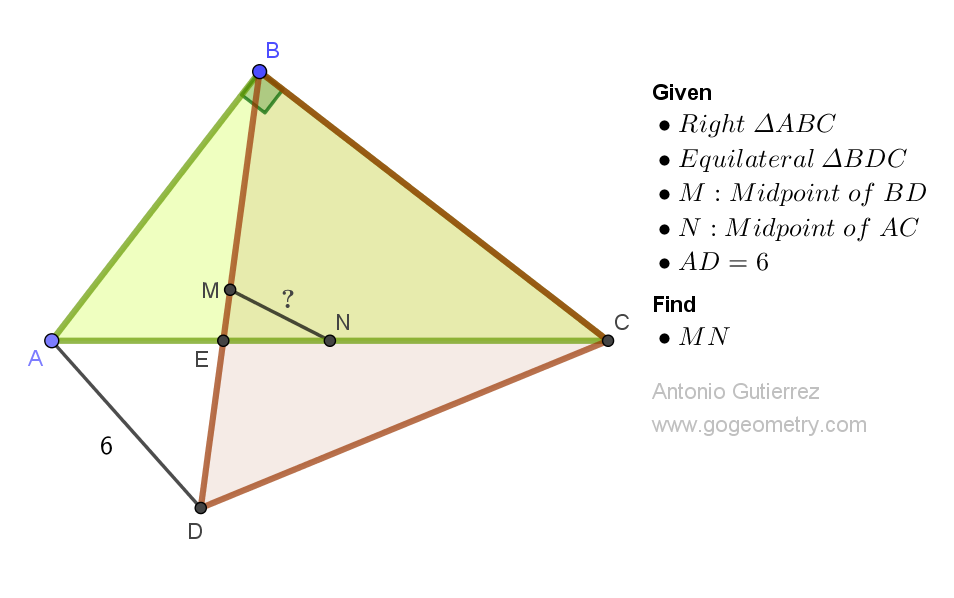
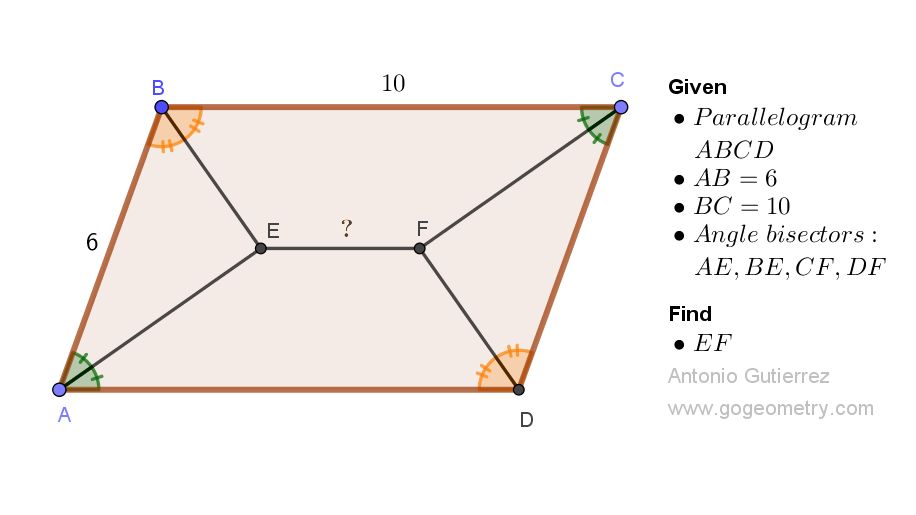
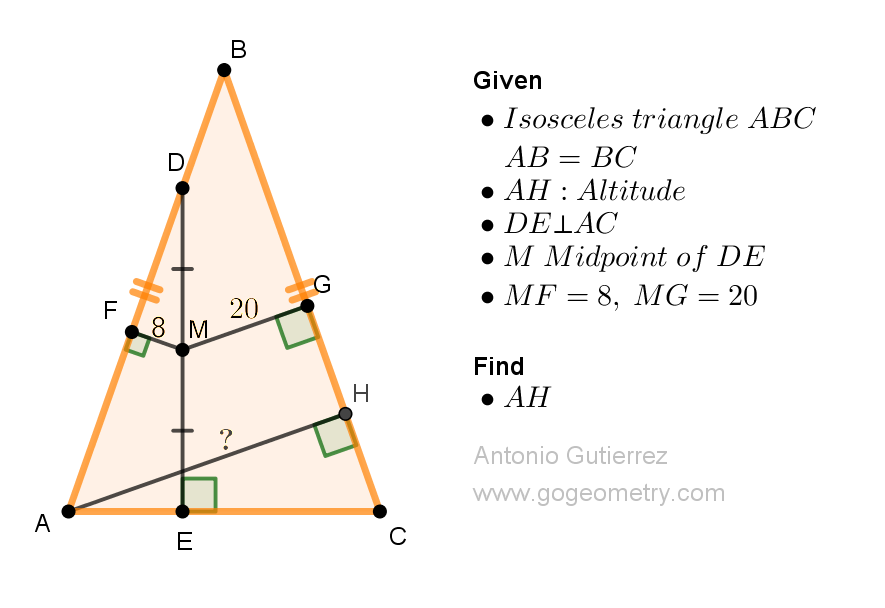
Geometry Problem 1526: Mastering Geometry Problem-Solving: Discover the Distance Between Two Sides in a Parallelogram Using Bisectors and Distance Measures. Difficulty Level: High School.

Given parallelogram ABCD with bisectors of angles A and D intersecting at point E, and the distance from E to AD measuring 10 units, determine the distance from A to CD in units.

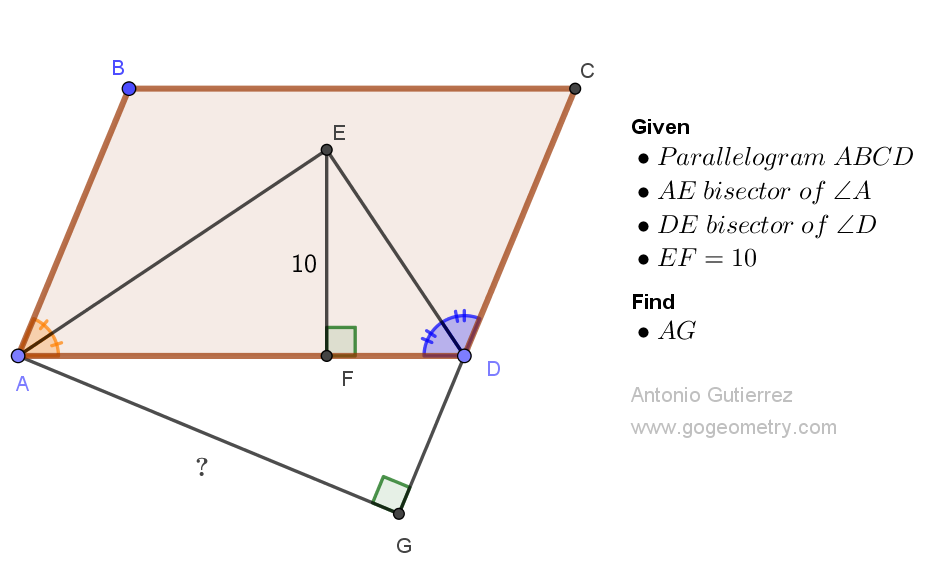
Geometry Problem 1526: Mastering Geometry Problem-Solving: Discover the Distance Between Two Sides in a Parallelogram Using Bisectors and Distance Measures

View or post a solution

Geometry Tips Now!

Concept Definition Theorem / Comment
Triangle A polygon with three sides and three angles. The sum of the angles in a triangle is 180 degrees.
Parallelogram A parallelogram is a quadrilateral with both pairs of opposite sides parallel. Opposite sides of a parallelogram are congruent; opposite angles are congruent; consecutive angles are supplementary; diagonals bisect each other.
Angle bisector A line or ray that divides an angle into two congruent angles.. The Angle Bisector Equidistant Theorem states that if a point lies on the angle bisector of an angle, then it is equidistant from the two sides of the angle.
Parallel lines Two lines in a plane that do not intersect. If two parallel lines are cut by a transversal, then the alternate interior angles are congruent, the corresponding angles are congruent, and the consecutive interior angles are supplementary.
Distance The distance between two geometric figures is generally defined as the minimum distance between any two points, one on each of the two figures..
Perpendicular lines Two lines or line segments that intersect at a right angle. Two lines perpendicular to a same line are parallel to each other.
Rectangle A rectangle is a two-dimensional shape with four straight sides and four right angles (90-degree angles). In a rectangle, opposite sides are congruent and parallel.
Congruence Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.. There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
Auxiliary line Auxiliary line is a line that is added to a diagram in order to help prove a theorem or solve a problem. Often, an auxiliary line is drawn to create additional congruent or similar triangles, to create parallel lines, or to create right angles. The use of auxiliary lines can simplify a problem or make a proof more straightforward. However, it is important to ensure that the auxiliary line does not create any new intersections or angles that were not present in the original diagram.
 

Discover Even More: See Also...

Problem 1527

Geometry Problem 1527: Discovering the Hidden Angle: Solving the Puzzle of Two Intersecting Circles

Problem 1525

Geometry Problem 1525: Unveiling the Secrets of Equilateral Triangles in Right Triangle Geometry: Finding the Midpoint Distance between Segments

Problem 1524

Geometry Problem 1524: Unlock the Mystery of Parallelograms: Discover the Length of Segment between the Intersecting Angle Bisectors

Problem 1523

Geometry Problem 1523: Discover How to Calculate the Length of the Altitude in an Isosceles Triangle - Get Expert Geometry Tips Now!

Problem 1522

Geometry Problem 1521: UUnlocking the Angle Measure of a Triangle with Median and Doubled Side Lengths. Difficulty Level: High School.

Problem 1521

Geometry Problem 1521: Unlock the Secret to Finding the Measure of an Angle in a Triangle with Two Sides as Diameters of Circles. Difficulty Level: High School.

 

Thematic Poem:
Solve the Parallelogram Challenge with Bisectors and Distances

Amidst the lines and angles that we see,
A challenge awaits, a geometry mystery,
Mastering problem-solving, the key,
To unlock the secrets of symmetry.

A parallelogram, ABCD its name,
Bisectors and distances, the tools to claim,
Find the distance from A to CD,
With precision and skill, solve it with glee.

A journey of discovery, a quest to prevail,
With logic and reasoning, let us unveil,
The distance between two sides we seek,
A problem to solve, a victory to keep.

So take on the challenge, with courage and might,
As we journey together, towards problem-solving light,
Master geometry, unleash your potential,
With bisectors and distances, make the problem incidental.

If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.

Recent Additions

Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Parallelogram
Angle Bisector
Perpendicular lines
Parallel lines
Congruence
View or Post a solution 

Search our site with Google: