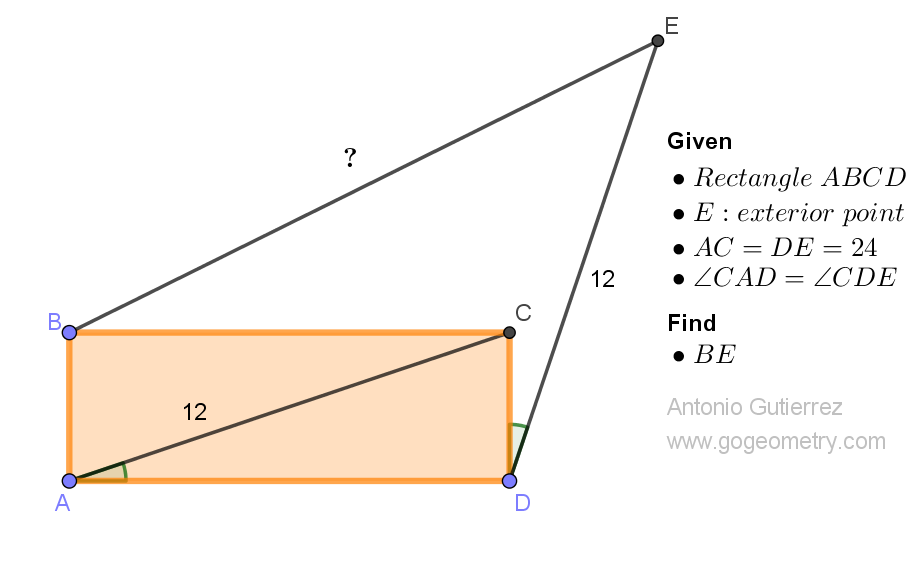
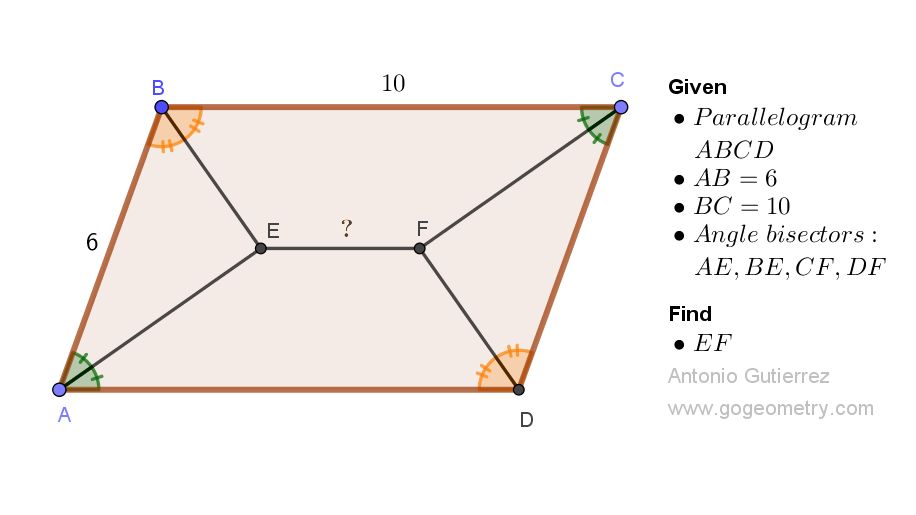
Geometry Problem 1524: Unlock the Mystery of Parallelograms: Discover the Length of Segment between the Intersecting Angle Bisectors. Difficulty Level: High School.
You are given a parallelogram ABCD with sides AB and BC measuring 6 and 10 units, respectively. The bisectors of angles A and B intersect at point E, and the bisectors of angles C and D intersect at point F. Find the length of segment EF.
View or post a solution
Geometry Tips Now!
| Concept | Definition | Theorem / Comment |
|---|---|---|
| Triangle | A polygon with three sides and three angles. | The sum of the angles in a triangle is 180 degrees. |
| Isosceles triangle | An isosceles triangle is a triangle that has two sides of equal length. | In an isosceles triangle, the altitudes relative to congruent sides are congruent. |
| Parallelogram | A parallelogram is a quadrilateral with both pairs of opposite sides parallel. | Opposite sides of a parallelogram are congruent; opposite angles are congruent; consecutive angles are supplementary; diagonals bisect each other. |
| Angle bisector | A line or ray that divides an angle into two congruent angles.. | |
| Parallel lines | Two lines in a plane that do not intersect. | If two parallel lines are cut by a transversal, then the alternate interior angles are congruent, the corresponding angles are congruent, and the consecutive interior angles are supplementary. |
| Congruence | Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.. | There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria. |
| Auxiliary line | Auxiliary line is a line that is added to a diagram in order to help prove a theorem or solve a problem. | Often, an auxiliary line is drawn to create additional congruent or similar triangles, to create parallel lines, or to create right angles. The use of auxiliary lines can simplify a problem or make a proof more straightforward. However, it is important to ensure that the auxiliary line does not create any new intersections or angles that were not present in the original diagram. |
Discover Even More: See Also...
Problem 1525
Problem 1523
Problem 1522
Problem 1521
Problem 1520
Problem 1519
Thematic Poem:
The Wonders of Parallelograms and Geometry Theorems
In geometry, we learn of shapes,
And theorems to
guide our way,
Parallelogram, a figure so sleek,
Has parallel sides that always stay.
Opposite sides and angles, congruent too,
Consecutive angles, supplementary for sure,
Diagonals
bisect each other, it's true,
In a parallelogram, we
can ensure.
Angle bisectors divide an angle in two,
Creating
congruent angles on either side,
A helpful tool to
solve problems anew,
In geometry, it's a joyride.
Parallel lines never meet,
In a plane, they
stretch far and wide,
Alternate interior angles
congruent,
A theorem that we can't hide.
Congruence is a notion so grand,
When triangles
are the same,
All sides and angles correspond,
Proving it can be our aim.
Auxiliary lines are a guiding light,
Helping us in
our geometry quest,
Creating triangles, parallel
lines, just right,
Making proofs easier and theorems
the best.
If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.
Recent Additions
Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Isosceles Triangle
Parallelogram
Angle Bisector
Midpoint
Perpendicular lines
Parallel lines
Congruence
View or Post a solution
Search our site with Google: