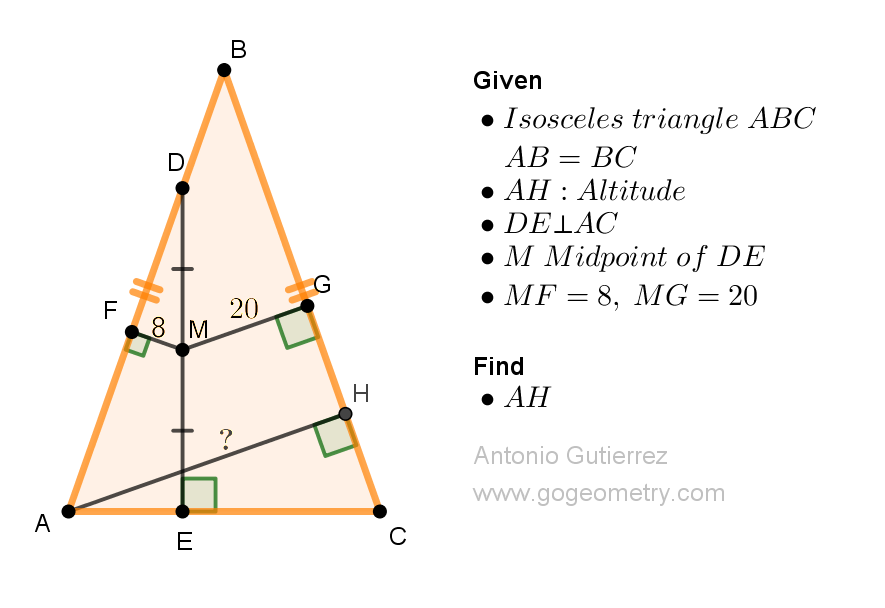
Geometry Problem 1523: Discover How to Calculate the Length of the Altitude in an Isosceles Triangle - Get Expert Geometry Tips Now! Difficulty Level: High School.

Given an isosceles triangle ABC with AB = BC, let AH be the altitude from A and let D be a point on AB. Let DE be perpendicular to AC with E lying on AC, and let M be the midpoint of DE. If the distance from M to AB is 8 units and the distance from M to BC is 20 units, determine the length of AH.

Geometry Problem 1523: Discover How to Calculate the Length of the Altitude in an Isosceles Triangle - Get Expert Geometry Tips Now!

View or post a solution

Geometry Tips Now!

Concept Definition Theorem
Triangle A polygon with three sides and three angles. The sum of the angles in a triangle is 180 degrees.
Isosceles triangle An isosceles triangle is a triangle that has two sides of equal length. In an isosceles triangle, the altitudes relative to congruent sides are congruent.
Midpoint The point that divides a line segment into two equal parts. The midpoint theorem for triangles, also known as the mid-segment theorem, states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half of its length.
Perpendicular lines Two lines or line segments that intersect at a right angle. Two lines perpendicular to a same line are parallel to each other.
Parallel lines Two lines in a plane that do not intersect. If two parallel lines are cut by a transversal, then the alternate interior angles are congruent, the corresponding angles are congruent, and the consecutive interior angles are supplementary.
Rectangle A rectangle is a two-dimensional shape with four straight sides and four right angles (90-degree angles). In a rectangle, opposite sides are congruent and parallel.
Congruence Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.. There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
 

Discover Even More: See Also...

Problem 1524

Geometry Problem 1524: Unlock the Mystery of Parallelograms: Discover the Length of Segment between the Intersecting Angle Bisectors

Problem 1522

Geometry Problem 1521: UUnlocking the Angle Measure of a Triangle with Median and Doubled Side Lengths. Difficulty Level: High School.

Problem 1521

Geometry Problem 1521: Unlock the Secret to Finding the Measure of an Angle in a Triangle with Two Sides as Diameters of Circles. Difficulty Level: High School.

Problem 1520

Geometry Problem 1520: Discovering Distances in a Rectangle with an Exterior Point: A Geometry Challenge. Difficulty Level: High School.

Problem 1519

Geometry Problem 1519: Discover the Length of a Segment in a Parallelogram using Midpoints and Parallel Lines. Difficulty Level: High School.

Problem 1518

Geometry Problem 1518: Boost Your Geometry Skills: Solve for the Number of Sides in an Equiangular Polygon with an Interior Point and Bisected Angle. Difficulty Level: High School.

Thematic Poem:
The Geometry of Symmetry: A Poem on Isosceles Triangles and Altitudes

In a triangle, isosceles and bright
An altitude soars in dazzling flight
Perpendicular, a line so true
From a point on base, it splits in two

Midpoint of this line, a beacon bright
With perfect symmetry, it shines with might
Distances from this midpoint, oh so clear
To the sides, a measure far and near

With these pieces laid before your eyes
The length of the altitude you'll devise
A puzzle to solve with care and thought
A triumph to gain, a lesson taught

In geometry, the beauty we find
A poetic dance of the heart and mind
A world of shapes and lines so true
A tapestry woven with a vibrant hue.

If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.

Recent Additions

Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Isosceles Triangle
Altitude
Midpoint
Perpendicular lines
Parallel lines
Rectangle
Congruence
View or Post a solution 

Search our site with Google: