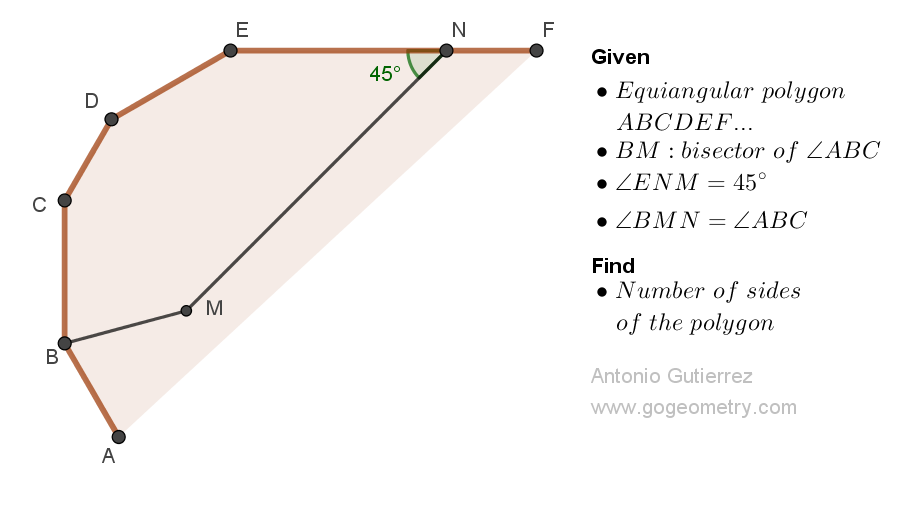
Geometry Problem 1518: Boost Your Geometry Skills: Solve for the Number of Sides in an Equiangular Polygon with an Interior Point and Bisected Angle.
In the figure shown, ABCDEF... is an equiangular polygon. M is an interior point, and N is a point on EF such that BM is the angle bisector of angle ABC, angle ENM measures 45 degrees, and angles BMN and ABC are congruent. Calculate the number of sides of the polygon.
Definitions and Suggestions
| Geometric Element | Definition/Theorem |
|---|---|
| Equiangular polygon | A polygon is equiangular if all its angles are congruent. |
| Convex polygon | A polygon is convex if every line segment connecting any two points inside the polygon lies entirely inside the polygon. The sum of the interior angles of an n-sided convex polygon is (n-2) * 180 degrees. |
Thematic Poem:
Equiangular Polygon and the Elegance and Power of
Geometry
In the realm of shapes and lines,
Where angles and edges
intertwine,
There lies a polygon, convex and fine,
Whose
properties are truly divine.
Equiangular it stands, with every angle equal,
A regularity that
makes it truly special,
Its sides are straight and its form is neat,
A polygon whose beauty is hard to beat.
But what of its angles, how many do they make?
A mystery that only
geometry can take,
The sum of its interior angles, so we're told,
Is a formula that never grows old.
Take its sides, subtract two,
Multiply by one eighty, and it's
true,
The sum of its angles, we can find,
And with this knowledge,
we're no longer blind.
So let us ponder this polygon so grand,
With its equiangularity
and angles so bland,
For in its simplicity, we can see,
The
elegance and power of geometry.