Geometry Problem 1517: Unlocking Triangle Side Length: Solving with a Median and Two Angles. Difficulty Level: High School.
In triangle ABC, BD is a median, and angles ABD and DBC measure 45 and 60 degrees, respectively. If BC measures 2, calculate the length of AB.
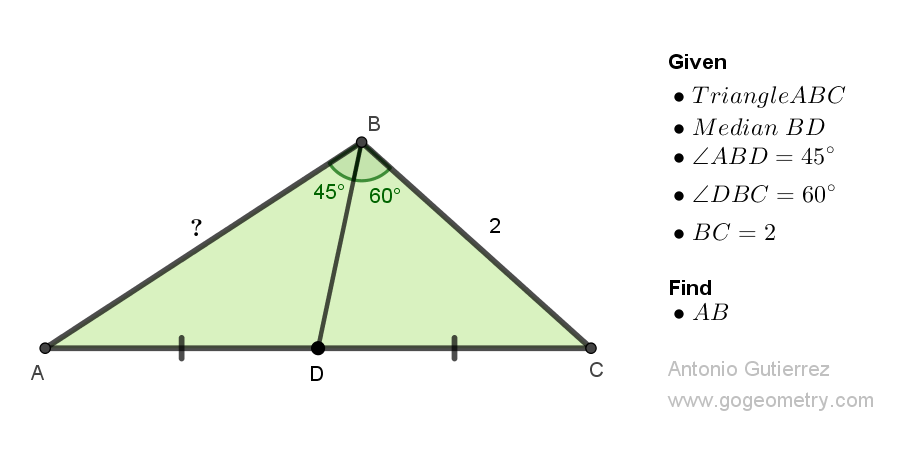
Definitions and Suggestions
| Geometric Element | Theorem Statement |
|---|---|
| 30-60-90 Triangle Theorem | In a 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is the square root of 3 times the length of the shorter leg. |
| 45-45-90 Triangle Theorem | In a 45-45-90 triangle, the length of the hypotenuse is the square root of 2 times the length of either leg. |
| Median Definition | In a triangle, the median from a vertex divides the opposite side into two segments of equal length. |
| Midsegment Theorem | In a triangle, the midsegment connecting the midpoints of two sides is parallel to the third side and half its length. |
Thematic Poem:
Unlocking Triangle Side Length with a Median and Two Angles
Unlocking triangle side length
A puzzle that seems to have no end
But with a median and two angles to tend
The solution we can
apprehend.
The median divides the triangle in two
And gives us angles to
eschew
With symmetry as our cue
We can find the missing sides
anew.
Geometry comes to our aid
To solve for the length of the blade
And with the angles that we've made
The answer is found, no need to
persuade.
Unlocking triangle side length
With a median and angles to
represent
We see the beauty of math's extent
And the solutions it
can present.