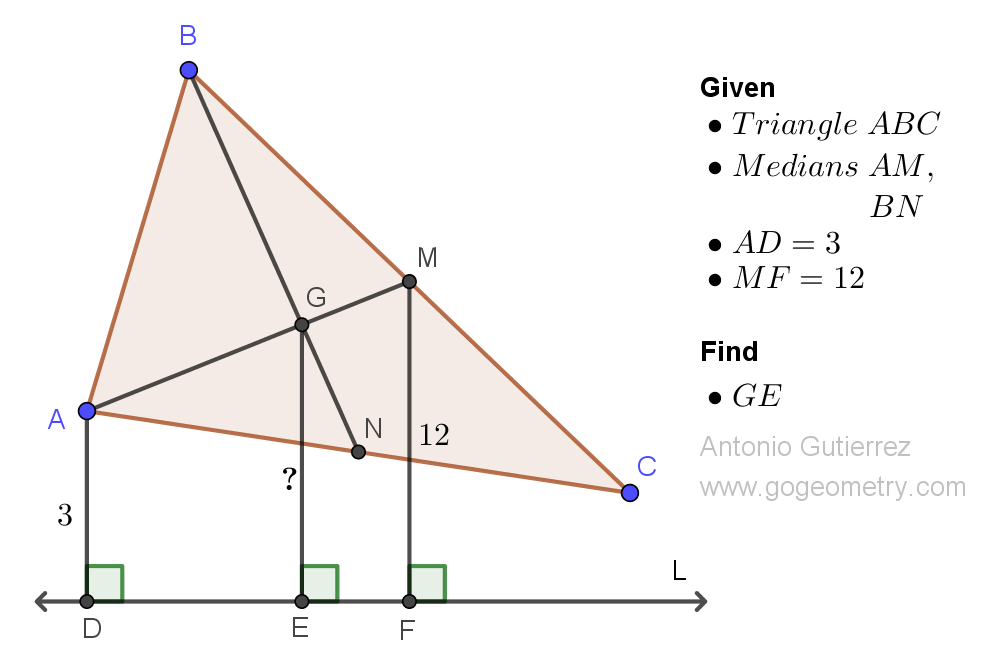
Geometry Problem 1515: Mastering Triangle Distance Calculation: Find the Distance from the Intersection of Medians to an Exterior Line. Difficulty Level: High School.

In triangle ABC, the point where the medians AM and BN intersect is called G. Given that the distance from point A to an exterior line L is 3 units and the distance from point M to L is 2 units, find the distance from point G to line L.

Definitions and Suggestions

• A triangle is a polygon that has three sides, three vertices, and three angles. Triangles are some of the most basic shapes in geometry and can be found in many different forms.
• A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.
• The distance between a point and a line is the length of the perpendicular segment drawn from the point to the line. This distance is also called the shortest distance or perpendicular distance.
• Perpendicular lines are two lines that intersect at a right angle (90 degrees).
• Parallel lines are lines in a plane that never intersect. They are always the same distance apart and will never converge or diverge.
• The median of a trapezoid is parallel to the bases of the trapezoid, and its length is equal to the average of the lengths of the bases.
• The centroid is the point of intersection of the three medians of a triangle, and is often referred to as the "center of gravity" or "center of mass" of the triangle.
• The Centroid Theorem states that the centroid of a triangle divides each of its medians into two segments, with the length of the segment closer to the vertex being twice as long as the length of the segment closer to the opposite side

View or post a solution