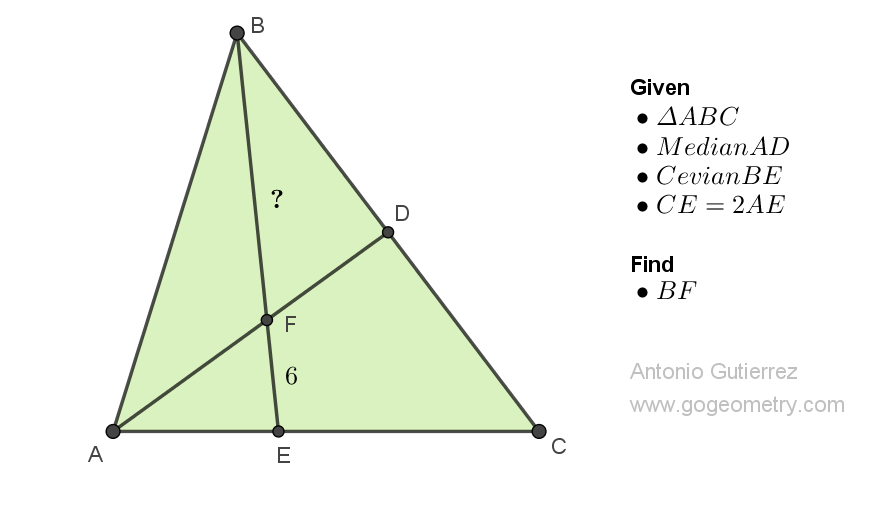
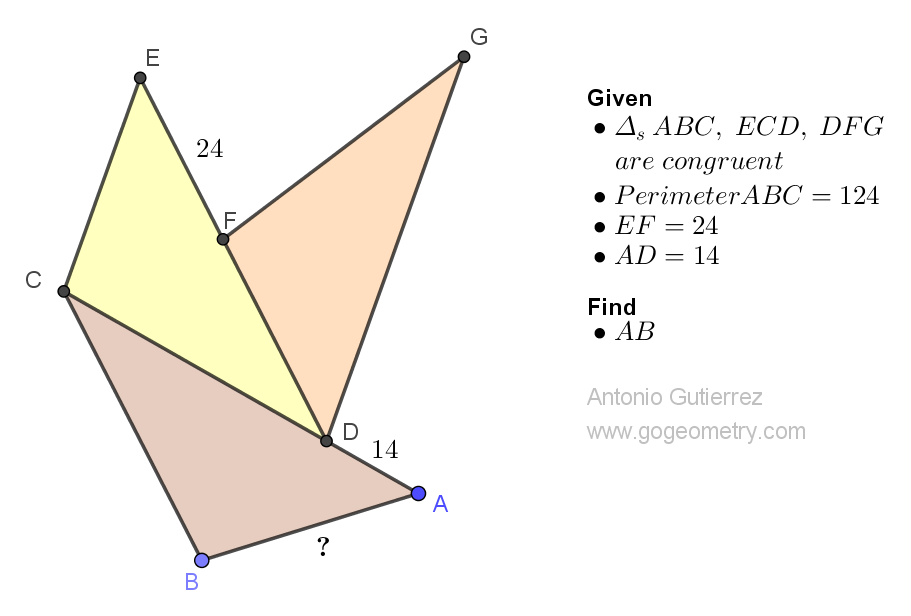
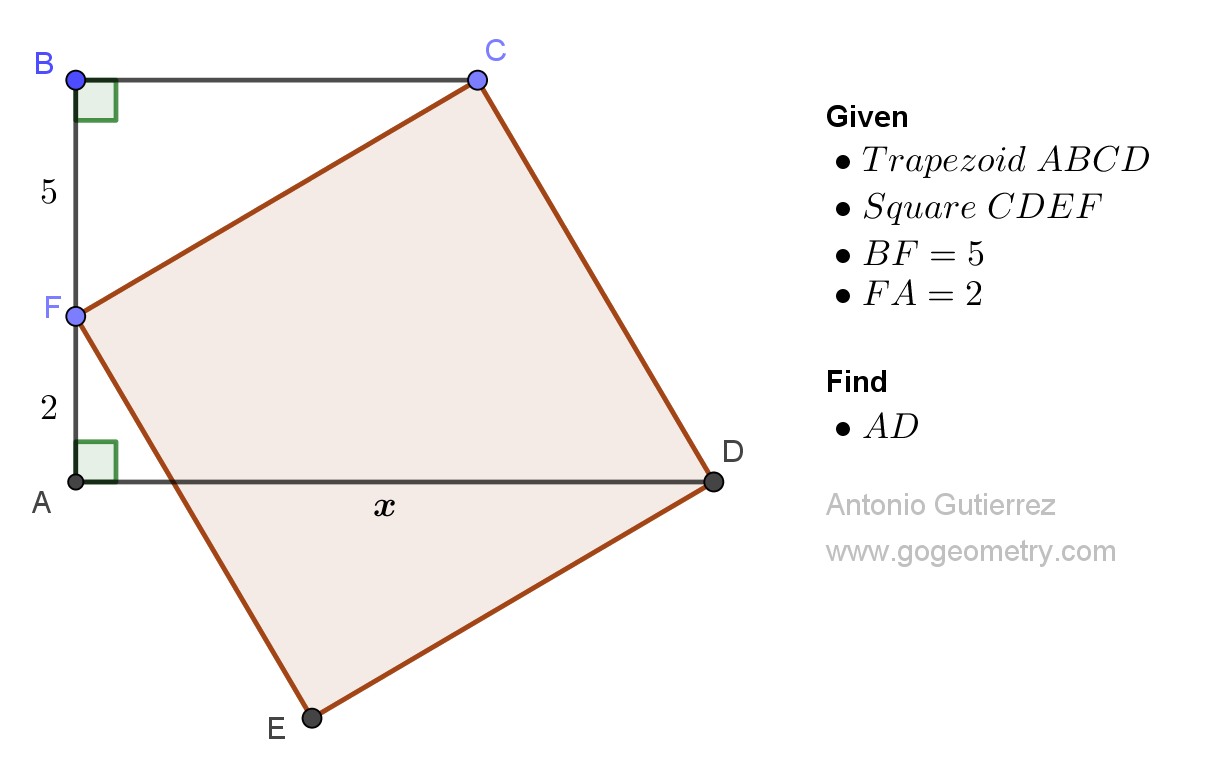
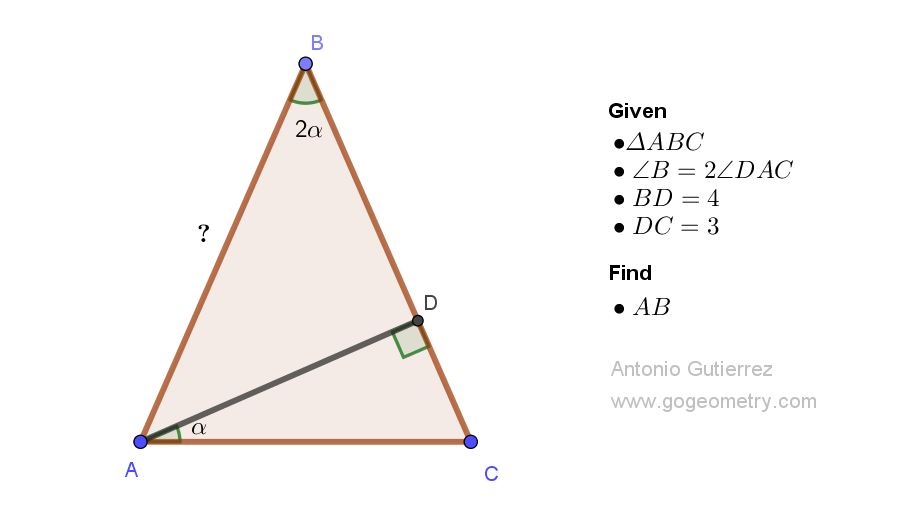
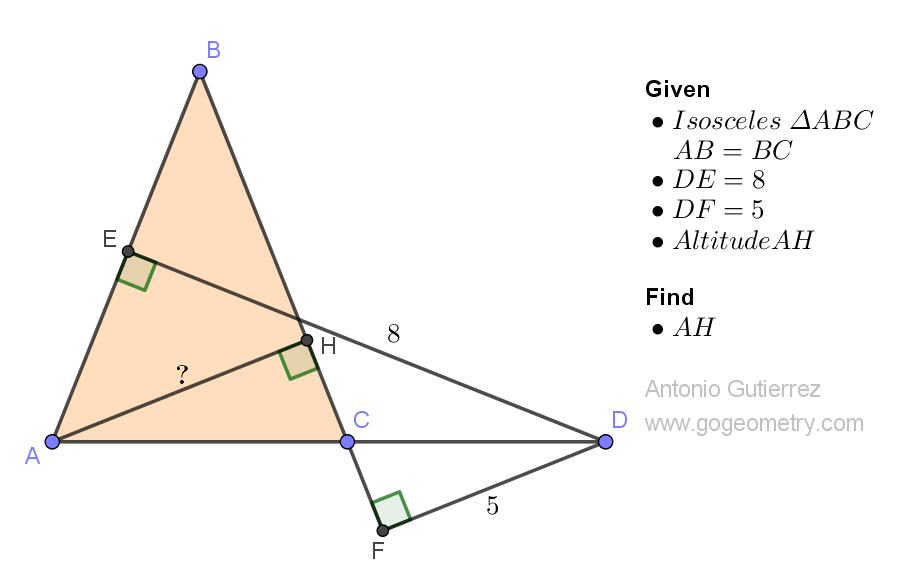
Geometry Problem 1511: Finding the Altitude of an Isosceles Triangle Using Distances from a Point on the Extension of the Base. Difficulty Level: High School.
Consider the isosceles triangle ABC shown in the figure below, where AB = BC. Let D be a point on the extension of AC, with distances of 8 and 5 from D to AB and BC, respectively. Find the length of the altitude AH.
Definitions and Suggestions
- A triangle is a polygon that has three sides, three vertices, and three angles. Triangles are some of the most basic shapes in geometry and can be found in many different forms.
- An isosceles triangle is a type of triangle that has two sides of equal length and two angles opposite those sides of equal measure.
- The base of an isosceles triangle is the side of the triangle that is not congruent to the other two sides.
- The distance from a point to a line is the length of the perpendicular line segment that connects the point to the line.
- Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle. There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
View or post a solution
Discover Even More: See Also...
Problem 1512
Problem 1510
Problem 1509
Problem 1508
Problem 1507
Problem 1506
Thematic Poem: Geometry and Symmetry: Discovering Altitude in an Isosceles Triangle
In an isosceles triangle with legs of equal length,
We seek the altitude with mathematical strength,
Using distances from a point on base extension's trail,
To find the height that will never fail.
With precision, we measure the lengths we need,
And draw perpendicular lines with great speed,
From the point to the legs, we calculate true,
The altitude that will come into view.
The line that we draw to the leg in question,
Marks the height with great precision,
And we marvel at the symmetry so clear,
Of the isosceles triangle that we revere.
Oh, how geometry can guide us so well,
To find the height that we need to tell,
In the isosceles triangle, with beauty so rare,
The altitude we find, we'll always have there.
If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.
Recent Additions
Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Isosceles Triangle
Congruence
Perpendicular lines
View or Post a solution
Search our site with Google: