Geometry Problem 1510: Congruence of Triangles, Perimeter, Measurement. Difficulty Level: High School.
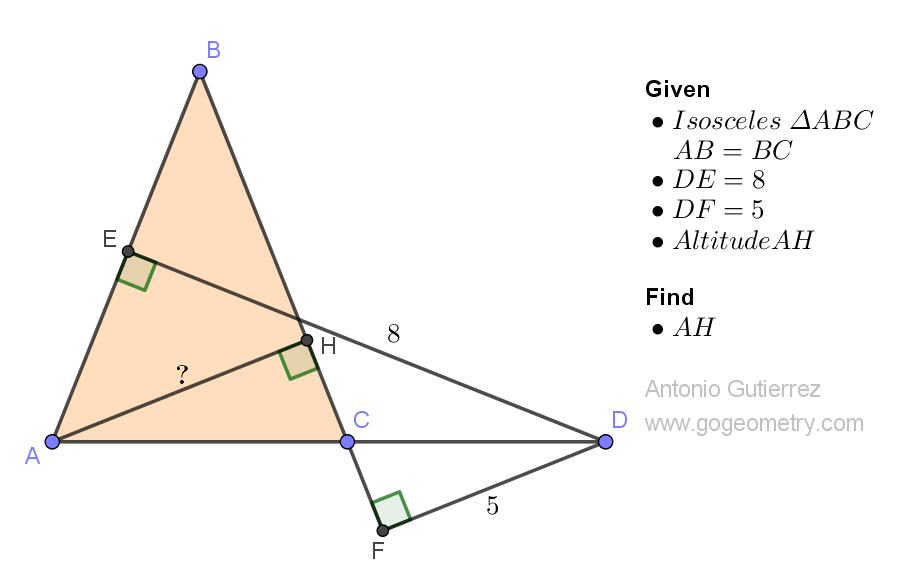
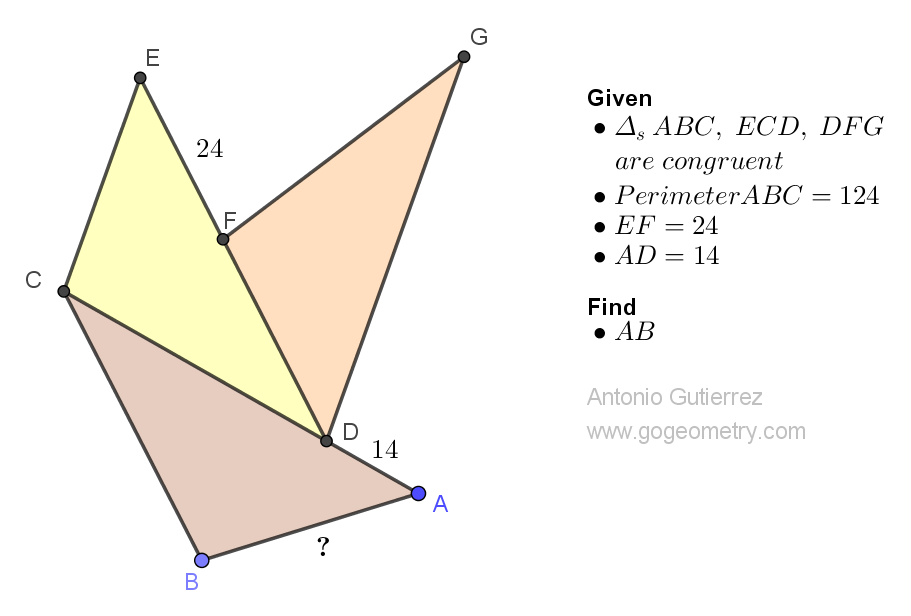
Given the figure where triangles ABC, ECD, and DFG are congruent, the perimeter of triangle ABC is 124 units, EF measures 24 units, and AD measures 14 units, find the length of AB in units.
Definitions and Suggestions
- A triangle is a polygon that has three sides, three vertices, and three angles. Triangles are some of the most basic shapes in geometry and can be found in many different forms.
- The perimeter of a triangle is the sum of the lengths of its three sides.
- Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle. There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
Poem: Congruent Triangles and Perimeter
Three triangles, congruent they are,
Equal in size, near or far,
Their perimeters, oh so grand,
Are equal, in every land.
The sides of each triangle match,
Equal in length, without a scratch,
Their angles too, a perfect match,
Three congruent triangles, what a catch!
To find the perimeter of this trio,
We add up the sides, oh so easy, though,
Three times the sum, we need to know,
And the answer will beautifully show.
Congruent triangles, a wonder to see,
In every shape, in every degree,
And through their congruence, we can see,
The beauty of math, in all its glory.