Geometry Problem 1509: Congruence of Triangles in a Trapezoid and a Square, Measurement. Difficulty Level: High School.
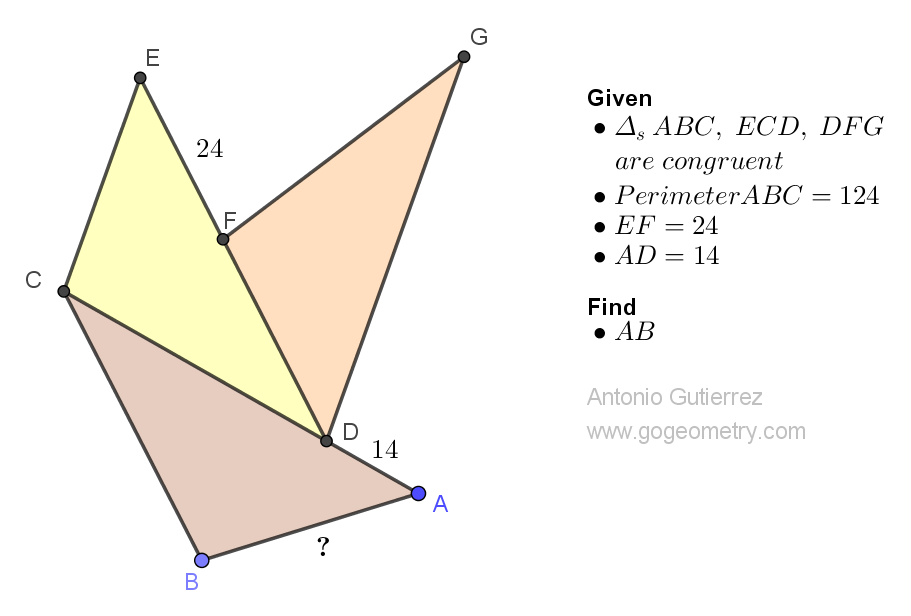
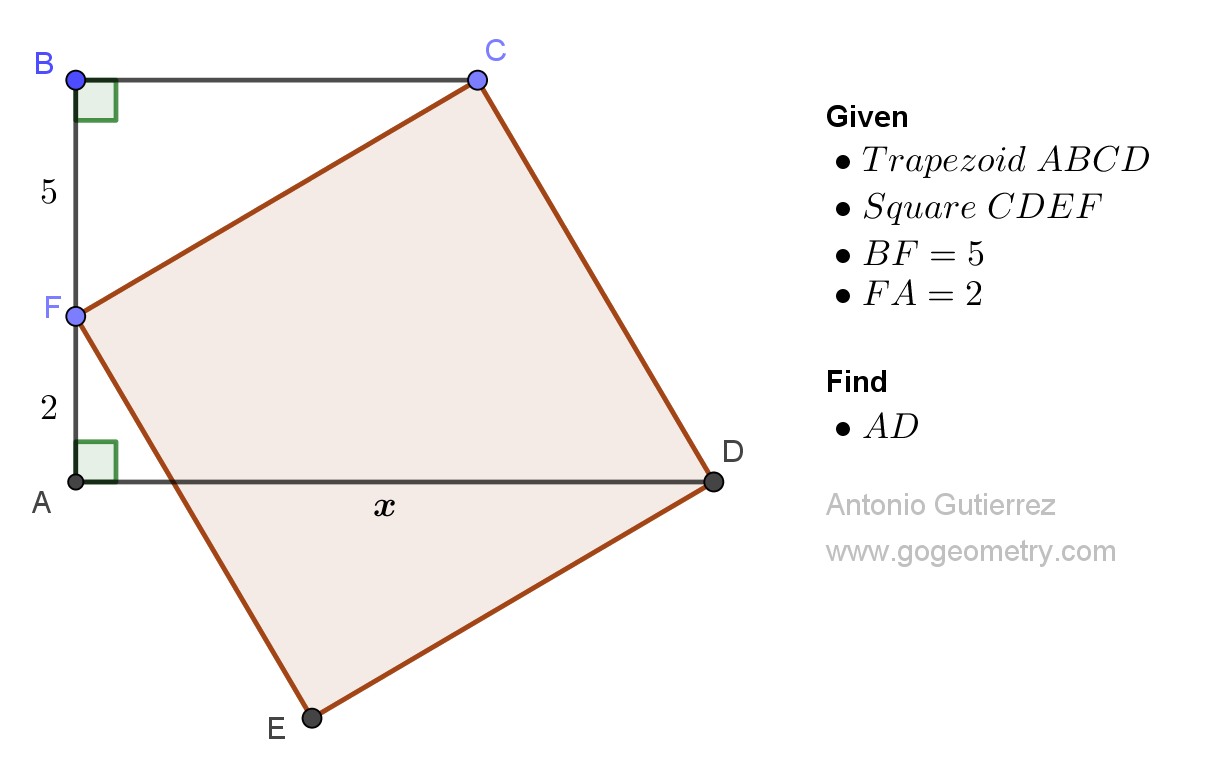
In the following figure, ABCD is a trapezoid and CDEF is a square such that F is on AB. If BF measures 5 units and FA measures 2 units, calculate the measure of AD.
Definitions and Suggestions
- A triangle is a polygon that has three sides, three vertices, and three angles. Triangles are some of the most basic shapes in geometry and can be found in many different forms.
- A trapezoid is a quadrilateral with at least one pair of parallel sides. Trapezoids are commonly encountered in geometry and in real-world applications, such as in architecture and engineering..
- A square is a special type of rectangle where all four sides are of equal length and all four angles are right angles (90 degrees). Squares are commonly used in geometry and in real-world applications, such as in tiling, flooring, and building construction.
- Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle. There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
Poem: Trapezoid, Square, and Congruence of Triangles
The trapezoid stands tall and proud,
With
parallel sides, it calls aloud.
Its height is long, and oh so high,
With angles meeting, it can't deny.
A square then comes to claim
its place,
On the trapezoid's height, with great grace.
Their
meeting point, they both have found,
And two right triangles now
abound.
Their congruence is plain to see,
With sides and
angles, all agreed.
The hypotenuses are the same,
And their
measurements, all quite tame.
In geometry, this congruence is
grand,
It helps us measure, plot, and plan.
We use it to build,
create, and design,
In all aspects, of our earthly shrine.
So
let us remember this tale so true,
Of a trapezoid and square,
together anew.
With congruent triangles, all in their place,
Geometry's beauty, we can embrace.