Geometry Problem 1522: Unlocking the Angle Measure of a Triangle with Median and Doubled Side Lengths. Difficulty Level: High School.
Consider a triangle ABC in which BD is the median, angle ABD is twice angle DBC, and BC is twice the length of BD. Find the measure of angle ABC.
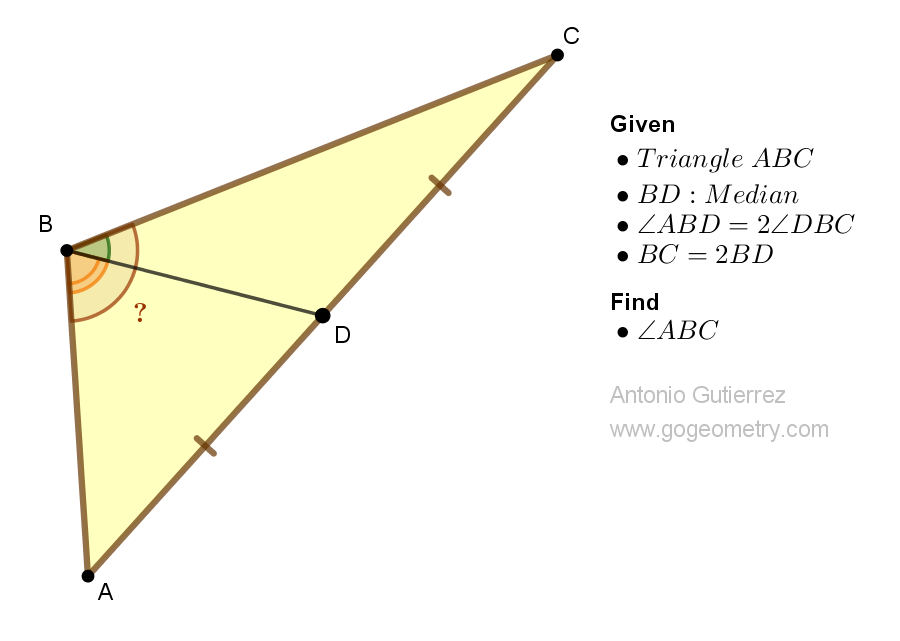
View or post a solution
Definitions and Suggestions
| Concept | Definition | Theorem |
|---|---|---|
| Triangle | A polygon with three sides and three angles. | The sum of the angles in a triangle is 180 degrees. |
| Median | A line segment that connects a vertex of a triangle to the midpoint of the opposite side. | In a triangle, the medians from any two vertices intersect at a point that is two-thirds of the way along the median from the vertex to the midpoint of the opposite side. |
| Midpoint | The point that divides a line segment into two equal parts. | The midpoint theorem for triangles, also known as the mid-segment theorem, states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half of its length. |
| Parallel lines | Two lines in a plane that do not intersect. | If two parallel lines are cut by a transversal, then the alternate interior angles are congruent, the corresponding angles are congruent, and the consecutive interior angles are supplementary. |
Thematic Poem:
Problem 1522:
Unveiling the Secrets of a Triangle: A Geometry Spree
In a triangle bold and true,
BD the median, divides it in two.
ABD angle twice DBC,
A fact that will set your geometry free.
BC doubled, BD too,
A puzzle that's challenging, but worth the
view.
The angle measure of ABC,
Is what we seek, for our geometry
spree.
Unlock the secrets of this shape,
Find the measure that's hidden
away.
Let your mind and compass guide,
And the angle measure will
no longer hide.
So measure and calculate with ease,
And discover the beauty that
geometry sees.
The angles of a triangle, we unveil,
A joyous
discovery, we now hail.
If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.
Recent Additions
Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Median
Midpoint
Parallel lines
View or Post a solution
Search our site with Google: