Geometry Theorems and Problems - Recent Additions (Page 11 of 15)

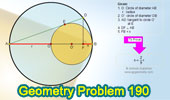Proposed Problem 190. Tangent circles, Tangent chord, Perpendicular, Distance.  

Proposed Problem 189. Squares, Distances.  

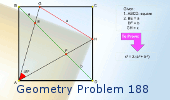Proposed Problem 188. Square, Diagonal, 45 Degrees Angle.  

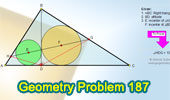Proposed Problem 187. Right Triangle, Altitude, Incenters, Circles, Angles.  

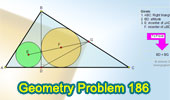Proposed Problem 186. Right Triangle, Altitude, Incenters, Circles.  

Proposed Problem 186. Right Triangle, Altitude, Incenters, Circles.  

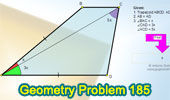Proposed Problem 185. Trapezoid, Triangles and Angles.  

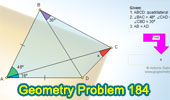Proposed Problem 184. Triangle and Angles.  

Proposed Problem 183. Right Triangle, Hypotenuse Trisection Points, Squares of the Distances.  

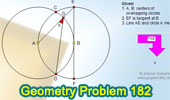Proposed Problem 182. Overlapping Circles, Find an angle.  

Proposed Problem 181. Circular Sector of 90 degrees, find an angle.  

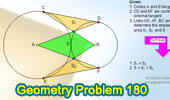Proposed Problem 180. Circles Tangent Externally, Common External Tangents, Areas.  

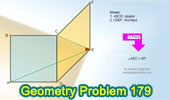Proposed Problem 179. Rhombus, Square, Diagonal, Angle.  

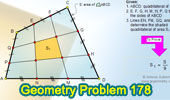Proposed Problem 178. Quadrilateral, Trisection of sides, Area.  

Proposed Problem 177. Parallelogram with Midpoints, Triangles, Areas.  

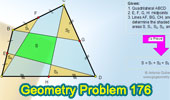Proposed Problem 176. Quadrilateral with Midpoints, Triangles, Areas.  

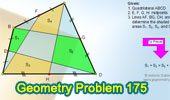Proposed Problem 175. Quadrilateral with Midpoints, Areas.  

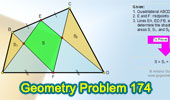Proposed Problem 174. Quadrilateral with Midpoints, Triangles, Areas.  

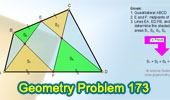Proposed Problem 173. Quadrilateral with Midpoints, Triangles, Areas.  

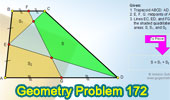Proposed Problem 172. Trapezoid, Midpoints, Quadrilaterals, Areas.  

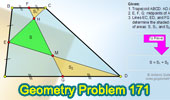Proposed Problem 171. Trapezoid, Midpoints, Triangles, Areas.  

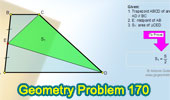Proposed Problem 170. Trapezoid, Midpoint, Triangle, Area.  

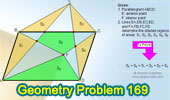Proposed Problem 169. Parallelogram, Interior and Exterior Points, Diagonals, Pentagon, Triangles, Areas  

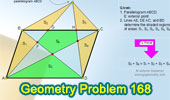Proposed Problem 168. Parallelogram, Diagonal, Triangles, Pentagon, Areas.  

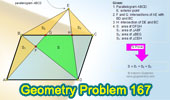Proposed Problem 167. Parallelogram, Diagonal, Triangles, Areas.  

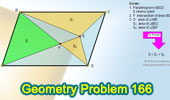Proposed Problem 166. Parallelogram, Diagonal, Triangles, Areas.  

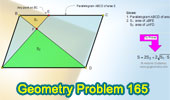Proposed Problem 165. Parallelogram, Diagonal, Triangles, Areas.  

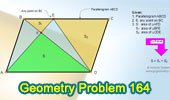Proposed Problem 164. Parallelogram, Trapezoid, Diagonal, Triangles, Areas.  

Proposed Problem 163. Trapezoid, Diagonals, Triangles, Areas.  
Trapezoid Index

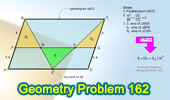Proposed Problem 162. Parallelogram, Triangles, Areas.  

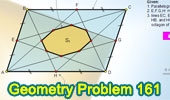Proposed Problem 161. Parallelogram, Midpoints, Octagon, Areas.  

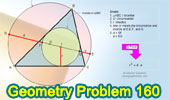Proposed Problem 160. Triangle, Incircle, Incenter, Circumcircle, Circumcenter, Inradius.  

Proposed Problem 159. Distances from the Circumcenter to the Incenter and the Excenters.  

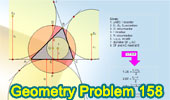Proposed Problem 158. Relation between the Circumradius, Inradius and Exradii of a triangle.  

Areas Index.

Congruence. Index.

Similarity, Ratios, Proportions. Index.

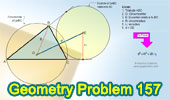Proposed Problem 157. Distance from the Circumcenter to the Excenter.  

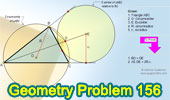Proposed Problem 156. Triangle, Circumradius, Exradius, Chord, Secant line.  

Proposed Problem 155. Euler's Theorem: Distance from the Incenter to the Circumcenter.  

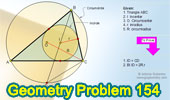Proposed Problem 154. Triangle, Inradius, Circumradius, Chord.

Proposed Problem 153. Circumscribed Quadrilateral, Diagonals Concurrent with Chords.  

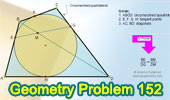Proposed Problem 152. Circumscribed Quadrilateral, Diagonal, Chord, Proportion.  

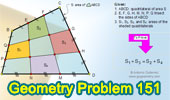Proposed Problem 151. Quadrilateral, Area, Trisection of Sides.  

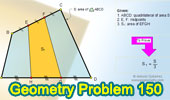Proposed Problem 150. Quadrilateral, Area, Trisection of Sides.

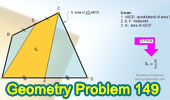Proposed Problem 149. Quadrilateral, Area, Midpoints.

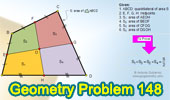Proposed Problem 148. Quadrilateral, Area, Midpoints.

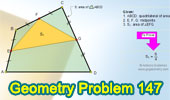Proposed Problem 147. Quadrilateral, Area, Midpoints, Triangle.

Proposed Problem 146. Varignon's Theorem: Quadrilateral, Midpoints, Parallelogram, Area, Perimeter.

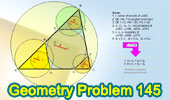Proposed Problem 145. Four Triangles, Incircle, Tangent and Parallel to Side, Incenters, Circumcenters.  

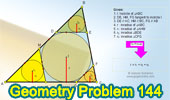Proposed Problem 144. Four Triangles, Incircle, Tangent and Parallel to Side, Inradii.

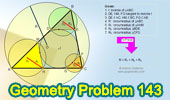Proposed Problem 143. Four Triangles, Incircle, Tangent and Parallel to Side, Circumradii.

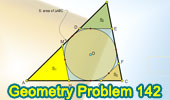Proposed Problem 142. Four Triangles, Incircle, Tangent and Parallel to Side, Areas.

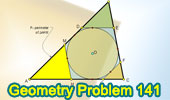Proposed Problem 141. Triangle, Incircle, Tangent , Parallel, Perimeters.

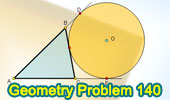Proposed Problem 140. Triangle, Excircle, Tangent, Semiperimeter.

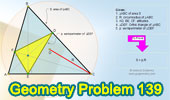Proposed Problem 139. Triangle Area, Orthic Triangle, Semiperimeter, Circumradius.  

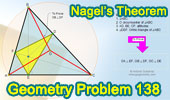Proposed Problem 138. Nagel's Theorem, Orthic Triangle, Altitudes, Circumradius, Perpendicular.  

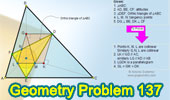Proposed Problem 137. Orthic Triangle, Altitudes, Perpendicular, Incircle, Collinear Points, Parallelogram.  

Proposed Problem 136. Orthic Triangle, Altitudes, Perpendicular, Concyclic Points.  

Proposed Problem 135. Orthic Triangle, Altitudes, Perpendicular, Parallel  

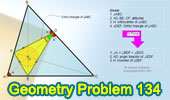Proposed Problem 134. Orthic Triangle, Altitudes, Angle Bisectors, Orthocenter, Incenter.  

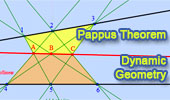Pappus Theorem. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.

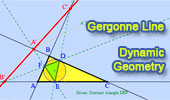Interactive Gergonne Line and Nobbs Points. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.

Interactive Simson Line. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.

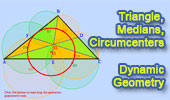Triangle, Medians, Six Circumcenters Concyclic. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.
Prove proposition.

Trapezoid, Triangle, Diagonals, Midpoints. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.
Prove proposition.

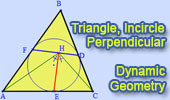Triangle: Incircle, Perpendicular, Angle Bisector. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.
Prove proposition.

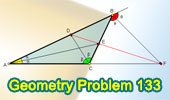Proposed Problem 133. Triangle, Angle Bisectors, Collinear Points.

Triangles. Theorems and problems about triangles.

Circles. Theorems and problems about circles.

Triangle Centers.

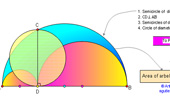Archimedes' Book of Lemmas

Quadrilaterals.

Adams' Circle Theorem.

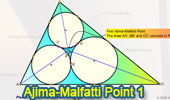First Ajima-Malfatti Point.

Second Ajima-Malfatti Point.

Apollonius' Tangency Problem for Three Circles Illustration with animation.

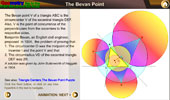The Bevan Point.

Heron's Formula. Key facts and a purely geometric step-by-step proof.

Johnson Theorem.

Kurschak's Tile and Theorem. Jozsef Kurschak (Hungary, 1864-1933) A square, with equilateral triangles. An elegant and a purely geometric way of finding the area of a regular dodecagon.
 

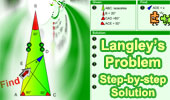Langley's Problem Adventitious angles. 20° isosceles triangle with animation.
 

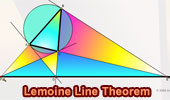Lemoine Theorem

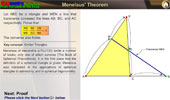Menelaus' Theorem.

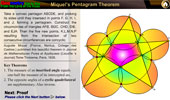Miquel's Pentagram Theorem Interactive proof with animation and key theorems.
 

Miquel's Pentagram with Dynamic Geometry. You can alter the pentagram dynamically in order to test and prove (or disproved) conjectures and gain mathematical insight that is less readily available with static drawings by hand. Requires Java Plug-in 1.3 or higher. Please be patient while the applet loads on your computer.

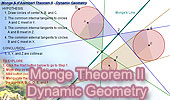Monge & d'Alembert Three Circles Theorem II with Dynamic Geometry. You can alter the geometric construction dynamically in order to test and prove (or disproved) conjectures and gain mathematical insight that is less readily available with static drawings by hand. Requires Java Plug-in 1.3 or higher. Please be patient while the applet loads on your computer.

Monge & d'Alembert Three Circles Theorem I with Dynamic Geometry. You can alter the geometric construction dynamically in order to test and prove (or disproved) conjectures and gain mathematical insight that is less readily available with static drawings by hand. Requires Java Plug-in 1.3 or higher. Please be patient while the applet loads on your computer.