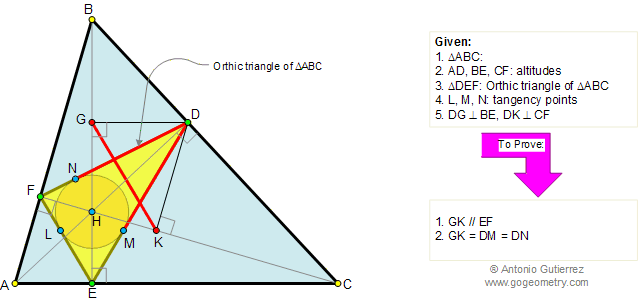
Geometry Problem 135. Orthic Triangle, Altitudes, Perpendicular, Parallel

In the figure below, given a triangle ABC and its orthic triangle DEF (AD, BE, and CF are the altitudes of ABC). L, M, N are the tangency points of the incircle of triangle DEF and DG and DK are perpendicular to BE and CF respectively. (1) Prove that GK is parallel to EF and (2) prove that GK = DM = DN. View or post a solution.