|
Take a pentagram ABCDE forming a convex pentagon
FGHIJ and
triangles AFJ, BGF, CHG, DIH, and EJI. Construct the circumcircles of triangles
AFJ, BGF, CHG, DIH, and EJI. Then the five new points, K,L,M,N,P
resulting from the intersection of two consecutive
circumferences are concyclic (lie on the same circumference).
Instructions: Dynamic Geometry (Requires
Java 1.3 or higher and Java enable browser)
You can alter the figure above
dynamically in order to test and prove (or disproved)
conjectures and gain mathematical insight that is less readily
available with static drawings by hand. To explore this theorem use the
replay buttons above to move step by step (1-2-3-4-5) through the
geometric construction:
-
 To
the Start (Step 1), To
the Start (Step 1),
 Jump
to next break (Step 2-3-4-5), Jump
to next break (Step 2-3-4-5),
 To the end.
To the end.
-
Manipulate the dynamic pentagram
by dragging the points
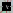 A,B,C,D,E
at any step. A,B,C,D,E
at any step.
-
The cursor keys (left, right,
up, down) move the picture. To give the keyboard focus to
the applet, click into it.
-
The + and - key change the size
magnification.
This page contains a
C.a.R. interactive geometry applet by R. Grothmann. Please be
patient while the applet loads on your computer. If you are using
a dial-up connection, it may take a couple minutes. If you get a warning-security asking 'Do you
want to trust the signed applet distributed by "Rene Grothmann"?'.
Please click 'Always', and you will not be troubled again.
If you can't see the presentation above, check a more recent
version of your browser. Alternately, it may be that your
browser supports Java, but that it’s currently set to disable
Java applets. Dynamic Geometry applet requires a Java Plug-in
1.3 or higherMore details at: http://www.java.com/en/download/help/index.jsp ).
Home | Sitemap |
Geometry
| Dynamic Geometry |
C.a.R.
|
Tessellations | Email
|