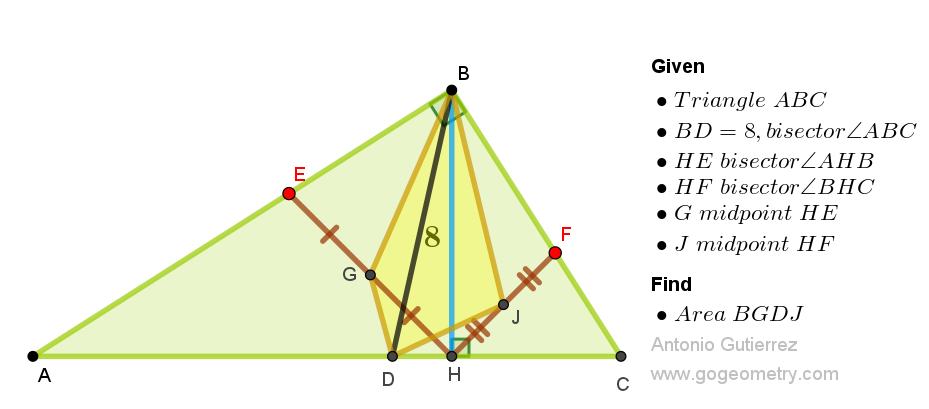
Geometry Problem 1564: Find the Area of Quadrilateral BGDJ in a Right Triangle involving the Altitude, Angle bisectors, and Midpoints.

In right triangle ABC (right angle at B), BD bisects angle ABC (BD = 8) and BH is the altitude to AC. Bisectors of angles AHB and BHC meet AB and BC at E and F respectively. G and J are midpoints of HE and HF. Find the area of quadrilateral BGDJ.

Diagram of right-angled triangle ABC with altitude, bisectors, and midpoint, quadrilateral area. Geometry Problem 1564.

Right triangle split,
Bisectors dance, midpoints meet,
Find BGDJ's shade.

Academic Levels: Suitable for High School and College Mathematics Education

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Vocabulary	Description
Right Triangle ABC	A triangle with a 90-degree angle at vertex B.
Bisector (BD)	A line segment that divides an angle into two congruent angles. In this case, BD divides angle ABC in half.
Altitude (BH)	A line segment drawn from a vertex (B) perpendicular to the opposite side (AC) in a triangle.
Right triangles (AHB & BHC)	The two smaller right triangles formed after drawing altitude BH. AHB has a right angle at H, and BHC has a right angle at H.
Bisectors (of AHB & BHC)	Line segments in triangles AHB and BHC that each divide their respective angles in half and intersect the opposite side.
Points (E & F)	The intersection points of the bisectors from AHB and BHC with sides AB and BC, respectively.
Midpoints (G & J)	The middle points of segments HE and HF, respectively.
Quadrilateral BGDJ	The four-sided figure formed by connecting points B, G, D, and J.