Geometry Problem 1558: The Midpoints of the Segments Connecting Corresponding Vertices of Equilateral Triangles Form an Equilateral Triangle

You are kindly requested to provide proof that: The midpoints of segments connecting corresponding vertices of equilateral triangles form an equilateral triangle.

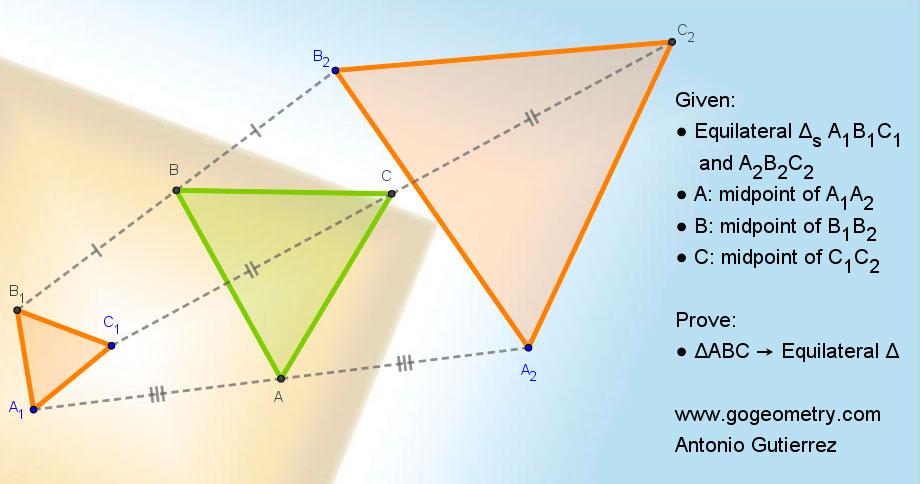
Illustration of Midpoints of lines connect Corresponding vertices of an equilateral triangle, A charming proof yields A hidden symmetry in geometry, Triangles three make one.

Midpoints of lines connect
Corresponding vertices of an equilateral triangle,
A charming proof yields
A hidden symmetry in geometry,
Triangles three make one.

Academic Levels: Suitable for High School and College Mathematics Education

Uncover and share solutions to this problem.

Read more, explore further

Geometry Problems
Open Problems
Visual Index
All Problems
Angles
Triangle
Equilateral Triangle
Midpoint
Congruence
View or Post a solution 

Discover Even More: See Also...

Problem 1559

Geometry Problem 1558

Problem 1557

Geometry Problem 1557

Problem 1556

Geometry Problem 1556

Problem 1555

Geometry Problem 1555

Search our site with Google: