Geometry Problem 1561: Triangle ABC, Circumcenter O, and Orthocenter H - A High School and College-Level Geometric Puzzle
In triangle ABC, with O as the circumcenter and H as the orthocenter, angle ABO is 21 degrees, and angle OBC is 42 degrees. Drawing a line parallel to BC from O, it intersects AC at point D. Determine the measure of angle DHC.
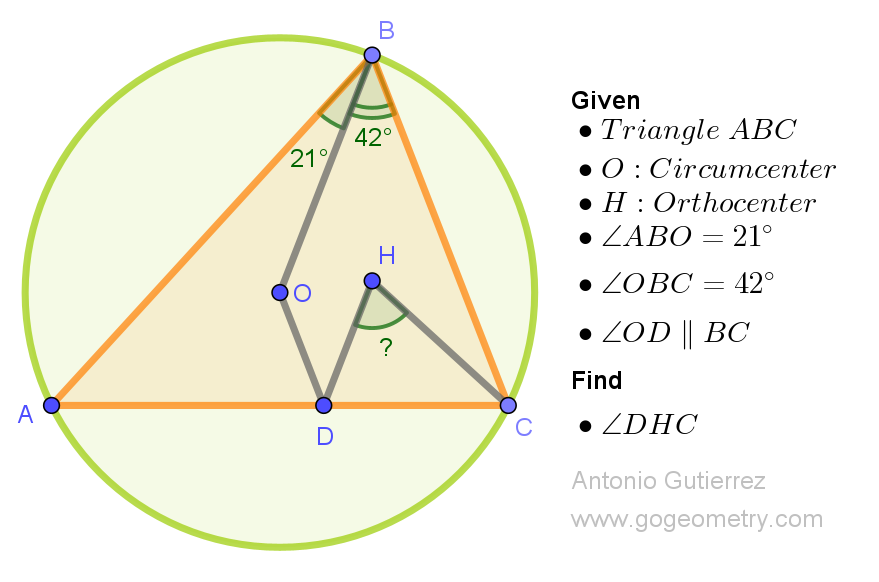
Circumcenter whispers,
Angles dance in sacred space,
O and H converge,
Parallel lines trace secrets,
DHC unfolds, mystique grows.
Academic Levels: Suitable for High School and College Mathematics Education
Uncover and share solutions to this problem.
Definitions and Suggestions
- A triangle is a polygon that has three sides, three vertices, and three angles. Triangles are some of the most basic shapes in geometry and can be found in many different forms.
- An angle is a figure formed by two rays, or half-lines, that have a common endpoint and extend in different directions.
- An altitude of a triangle is a line segment that is drawn from a vertex of a triangle perpendicular to the opposite side or to the line containing the opposite side.
- The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect. It is equidistant from the vertices of the triangle, making it the center of the circumcircle, which is the circle passing through all three vertices of the triangle.
- The orthocenter of a triangle is the point of intersection of its three altitudes.
- A central angle in a circle is formed by two radii (line segments from the center of the circle to any two points on its circumference). The measure of a central angle is equal to the angle subtended by the intercepted arc.
- An inscribed angle in a circle is formed by two chords (line segments connecting two points on the circle). The measure of an inscribed angle is half the measure of the intercepted arc.
- Parallel lines are two or more lines that are always the same distance apart and never intersect, regardless of how far they are extended. In Euclidean geometry, parallel lines have the same slope and will never converge. The symbol "||" is often used to denote parallel lines. Parallel lines play a crucial role in geometry, trigonometry, and other branches of mathematics.
- Suggestions:
The sum of the angles in a triangle is always 180 degrees, which is known as the Triangle Sum Theorem.
- In a triangle, if two angles are congruent, then the sides opposite those angles are also congruent.
Flyer of problem 1561 using iPad Apps
Read more, explore further
Geometry Problems
Open Problems
Visual Index
All Problems
Angles
Triangle
Circle
Circumcircle
Orthocenter
Parallel lines
Perpendicular lines
Diameter
Altitude
Isosceles Triangle
Double Angle
View or Post a solution
Discover Even More: See Also...
Problem 1562
Problem 1560
Problem 1559
Problem 1558
Problem 1557
Search our site with Google: