Online Geometry: Classical Theorems of Euclidean Geometry

Classical Theorems - Page 1

Dynamic Geometry 1478.
Cyclocevian, Reuschle-Terquem Theorem, Concurrent Cevians, Triangle, Circumcircle, Secant line, Step-by-step Illustration. GeoGebra, iPad.

Dynamic Geometry 1477.
Miquel's Pentagram Theorem, Pentagon, Triangle, Circumcircles, Concyclic Points, Step-by-step Illustration. GeoGebra, iPad.

Dynamic Geometry 1476.
Droz-Farny Line Theorem, Triangle, Orthocenter, Perpendicular, Collinear Midpoints, Step-by-step Illustration. GeoGebra, iPad.

Dynamic Geometry 1475.
Clifford Intersecting Circles Theorem, Step-by-step Illustration, GeoGebra, iPad.

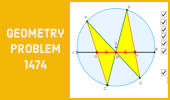Dynamic Geometry 1474.
Butterfly Theorem, Circle, Chords, Midpoints, Step-by-step Illustration.

Dynamic Geometry 1473.
Kosnita's Theorem, Triangle, Four Circumcenters, Concurrent Line, Step-by-step Illustration.

Dynamic Geometry 1468.
Steiner's Theorem, Triangle, Circumradius, Inradius, Sum of Exradii, Step-by-step Illustration.

Geometry Problem 1466.
Tangential Quadrilateral, Newton Line, Incenter, Midpoint, Diagonal, Collinear Points. Step-by-step Illustration using GeoGebra.

Geometry Problem 1462.
Newton-Line, Newton-Gauss Line, Complete Quadrilateral, Midpoints of Sides and Diagonals, Collinear Points. Step-by-step Illustration using GeoGebra.

Dynamic Geometry 1460.
Newton-Gauss Line, Complete Quadrilateral, Midpoints of Diagonals, Collinear Points, Step-by-step Illustration using GeoGebra.

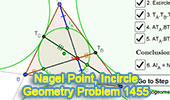Geometry Problem 1455.
Nagel Point, Excircles, Incircle, Congruent Segments, iPad. Step-by-step illustration using GeoGebra.

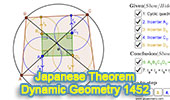Dynamic Geometry 1452.
Japanese Theorem, Sangaku, Cyclic Quadrilateral, Incenter, Rectangle, Inradius. Step-by-step illustration using GeoGebra.

Dynamic Geometry 1451.
Orthopole of a Line. Step-by-step illustration using GeoGebra.

Dynamic Geometry 1450.
Ortholine, Steiner Line, Complete Quadrilateral, Collineal Orthocenters. Step-by-step illustration using GeoGebra.

Dynamic Geometry 1449.
Salmon Line. Step-by-step illustration using GeoGebra.

Dynamic Geometry 1448.
Simson Line. Step-by-step illustration using GeoGebra.

Dynamic Geometry Problem 1447.
Outer Vecten Point. Step-by-step illustration using GeoGebra.

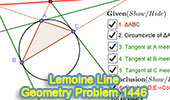Dynamic Geometry Problem 1446.
Lemoine Line, triangle, circumcircle, tangent, collinear points. Step-by-step animation using GeoGebra.

Dynamic Geometry Problem 1444.
The Asymmetric Propeller Theorem, Equilateral Triangles, Midpoints. Step-by-step animation using GeoGebra.

Pythagorean Theorem.

Euclid's Elements Book II, Proposition 12: Law of Cosines.

Euclid's Elements Book II, Proposition 13: Law of Cosines.

Median length, Apollonius' Theorem

The significance of the Pythagorean theorem by Jacob Bronowski.
Pythagorean Theorem, 47th Proposition of Euclid's Book I.

Carnot's Theorem. Geometry Problem 889
Carnot's Theorem in an acute triangle, Circumcenter, Circumradius, Inradius. GeoGebra, HTML5 Animation for Tablets.

Ceva's Theorem. Concurrency. Interactive proof with animation. Key concept: Menelaus Theorem. 

Menelaus' Theorem. Interactive proof with animation and key concepts..

van Aubel's Theorem. Quadrilateral with Squares. Proof with animation.

van Aubel's Theorem. Quadrilateral with Squares. Proof with animation for Tablets, iPad, Nexus, Galaxy.

Dynamic Geometry Problem 1445.
Van Aubel's theorem, Quadrilateral and Four Squares, Centers. Step-by-step animation using GeoGebra.

Heron's Formula.
Key facts and a purely geometric step-by-step proof.
 

Euclid's Elements Book I, 23 Definitions. One-page visual illustration.
Euclid's Elements Book. Index

Euclid's Elements Book VI, Proposition 3: Angle Bisector Theorem

Euclid's Elements, Book XIII, Proposition 10 One page visual illustration.

Ptolemy's Theorem.
 

Dynamic Geometry: Brahmagupta Theorem, . GeoGebra, HTML5 Animation for Tablets

Brianchon's Theorem in a Circumscribed Hexagon.

Brianchon Corollary, Circumscribed Hexagon, Concurrency lines.

Carnot's Theorem in an Acute Triangle.

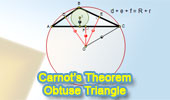Carnot's Theorem in an Obtuse Triangle.

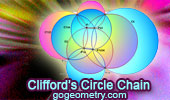Clifford's Circle Chain Theorems. This is a step by step presentation of the first theorem. Clifford discovered, in the ordinary Euclidean plane, a "sequence or chain of theorems" of increasing complexity, each building on the last in a natural progression.
 

Cyclic Quadrilateral: Ratio of the Diagonals
 

Nine-Point Center, Nine-Point Circle, Euler Line.
Interactive illustration.

Soddy Circles and Descartes Theorem.
Three tangent circles, Inscribed and Circumscribed Circles, Radii.

Euler's Problem, Problem 155. Distance between the Incenter to the Circumcenter.

The Simson Line, Theorems and Problems - Index.

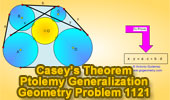Casey's Theorem. Generalized Ptolemy's Theorem.

Brahmagupta's Formula  Area of a cyclic quadrilateral.

Brahmagupta's Theorem Cyclic quadrilateral.

Platonic Solids, Interactive animation.
HTML5 Animation for iPad and Nexus
Flash Animation.

Theaetetus' Theorem, Platonic Solids, Interactive animation

Go to Page: Previous | 1 | 2 | 3 | 4 | 5 | Next