Geometry Challenge 1598: Inradius Ratio with Median BM in a Right-Angled Triangle
Test your geometry skills with this STEM-focused problem. Explore how the median BM, drawn to midpoint M of the hypotenuse, reveals a surprising inradius ratio in two splitting triangles.
Problem 1598 Statement
In triangle ABC, with AB = 3, BC = 4, and a right angle at B, let M be the midpoint of hypotenuse AC. Find the ratio of the inradii of triangles ABM and BMC.
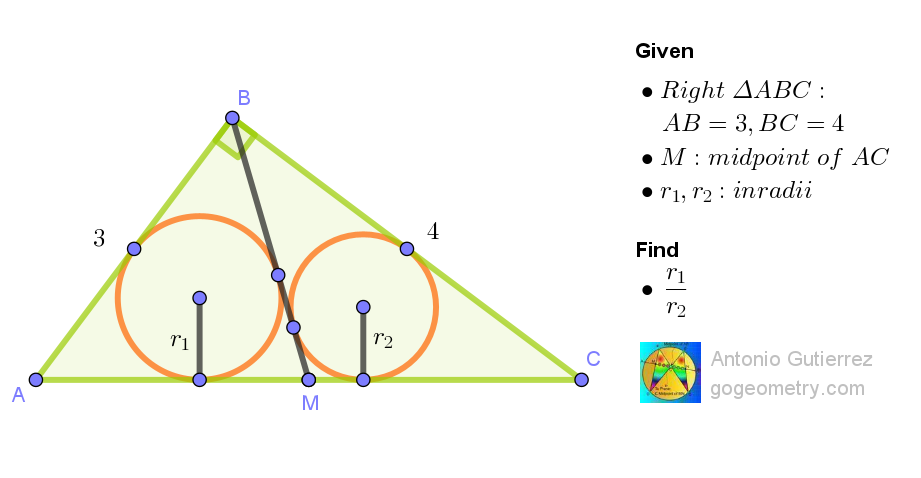
Median BM
Splits the heart of triangle,
Ratios bloom within.
STEM Approach 1598: Inradius Ratio with Median BM
Relate median BM to the center of mass in a uniform triangular plate.
Question: Where is the centroid along BM?
How would the inradii relate to areas and balancing forces?
Use Geogebra or Geometry Expressions or Desmos to model triangle ABC, draw BM, and compare inradii of ABM and BMC.
Compute and visually compare inradii of triangles ABM and BMC.
Explore how splitting a triangle with a median affects structural balance in frameworks and bridge supports.
In trusses and frameworks, medians and centroids determine stress points.
Connect to:
- Median length theorems
- Inradius and area relationships
- Pythagorean theorem
Inquiry: How does dividing by a median affect other properties?
STEM Geometry Challenge 1598: Unlock the Power of Problem-Solving!
