|
 A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist.
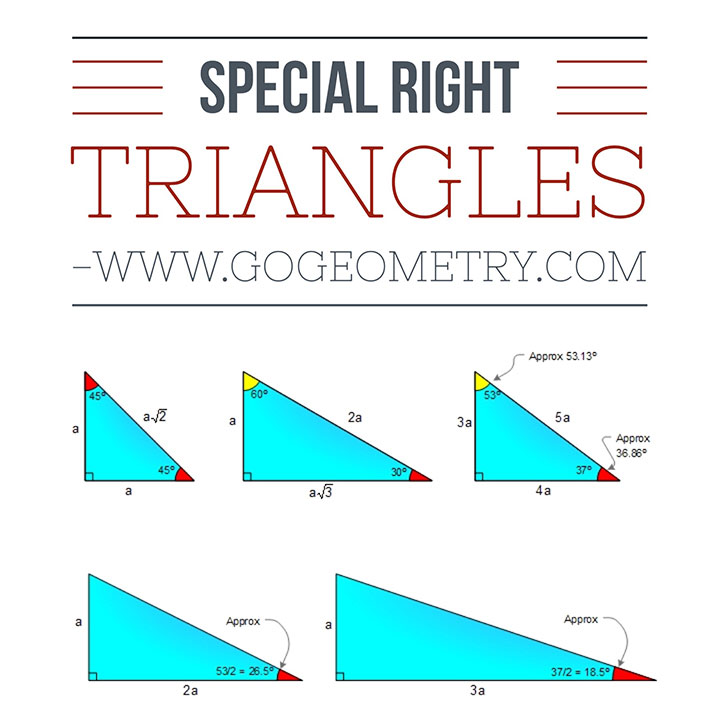
Angle based right triangle: 30-60-90, 45-45-90. (Angles that form a simple ratio)
Side based right triangle: 3-4-5 (The lengths of the sides form a whole number ratio),
approx angles 37-53.
Knowing the ratios of the angles or sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.
Special right triangles have many benefits when it comes to
solving geometry problems. Some of these benefits include:
-
Simplifying calculations: Special right triangles have specific
ratios of their sides, making them easier to work with and
simplifying calculations. For example, in a 45-45-90 triangle, the
ratio of the length of the legs to the length of the hypotenuse is
1:1:√2, which can make calculations involving the sides of the
triangle much simpler.
-
Facilitating problem-solving: Recognizing a special right
triangle in a geometry problem can make it much easier to solve. By
understanding the properties of special right triangles and how they
relate to other geometric concepts, students can quickly identify
the relevant information in a problem and use it to find the
solution.
-
Building a foundation for advanced math: Special right triangles
are a fundamental concept in geometry and lay the groundwork for
more advanced mathematical concepts, such as trigonometry and
calculus. By mastering special right triangles, students can build a
strong foundation for these more complex subjects.
-
Providing a real-world context: Special right triangles are used
in many real-world applications, such as in architecture and
engineering. By learning about special right triangles, students can
gain a better understanding of how math is used in the real world
and how it relates to their everyday lives.
Overall, special right triangles are a powerful tool in solving
geometry problems. By understanding their properties and how they relate
to other geometric concepts, students can simplify calculations, solve
problems more efficiently, and build a strong foundation for advanced
math.
|
