Geometry Problem 1535: Crack the Code: Inscribed Circle in Square - Angle Challenge! Solve the Mystery
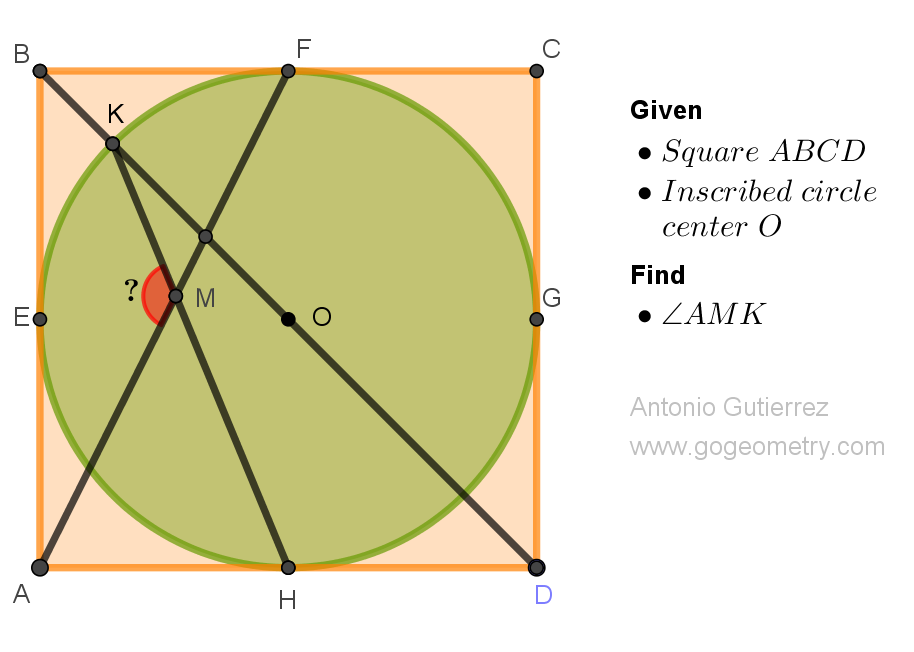
In a square ABCD, a circle with center O is inscribed, such that it touches sides AB, BC, CD, and AD at points E, F, G, and H, respectively. The line BD intersects the arc EF at point K. The lines AF and HK intersect at point M. Calculate the measure of angle AMK.
View or post a solution
Recent Additions
Geometry Problems
Open Problems
Visual Index
All Problems
Circle
Square
Triangle
Circle Tangent Line
Angle
Perpendicular lines
Special Right Triangle
Thematic Poems
View or Post a solution
Illustrating Problem 1535: A Creative Poster Using iPad Apps

Discover Even More: See Also...
Problem 1536
Problem 1534
Problem 1533
Problem 1532
Problem 1531
Problem 1530
Problem 1529
Thematic Poem:
Geometric Symphony: The Tale of a Square, a Circle, and Angle AMK
Within a square, so perfect and true,
A circle's
grace, a geometric view,
With center O, it stands
inscribed,
Touches sides with poise, in points
described.
AB, BC, CD, AD, it meets with ease,
At E, F, G,
and H, with gentle tease,
A symphony of shapes, in
harmonious blend,
A dance of lines, that seem to
never end.
The line BD, a path it takes,
Intersects the arc
with calculated stakes,
At point K, where angles
meet,
A junction formed, so sweetly neat.
AF and HK, two lines in play,
They intersect, in a
wondrous way,
At point M, where paths converge,
A
meeting point, a geometrical urge.
Now, angle AMK, the final quest,
A measure sought,
a mathematical test,
With skill and wit, calculations
made,
Solving the puzzle, with math displayed.
So, in this tale of squares and circles told,
A
poetic ode to geometry bold,
With lines and points,
and angles to see,
A mathematical journey, a
captivating decree.
If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.
Search our site with Google: