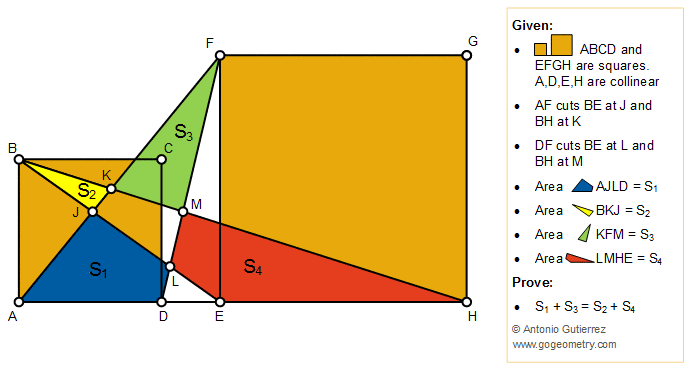
The figure below shows two squares ABCD and EFGH so that A, D, E, and H are collinear points. Line AF cuts BE at J and BH at K, Line DF cuts BE at L and BH at M. If area AJLD = S₁, area BKJ = S₂, area KFM = S₃, and area LMHE = S₄, prove that S₁ + S₃ = S₂ + S₄.
 

See solution below

---

Geometric Art of Problem 1426: Sketching, Typography, iPad Apps

See solution below

---

Animation of the Conformal Mapping or Transformation of Problem 1426

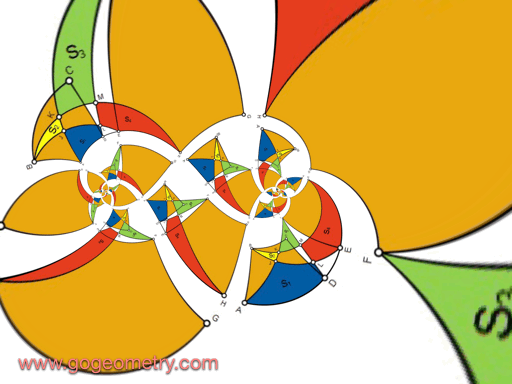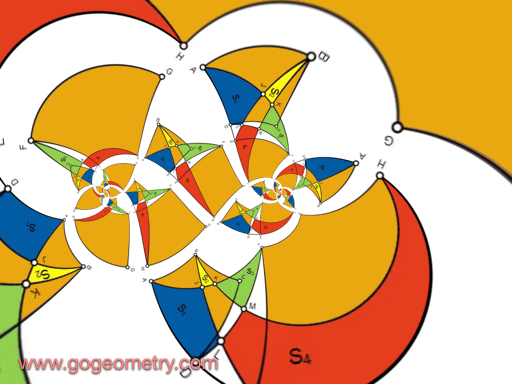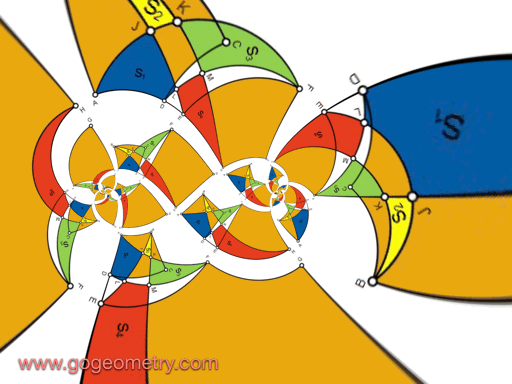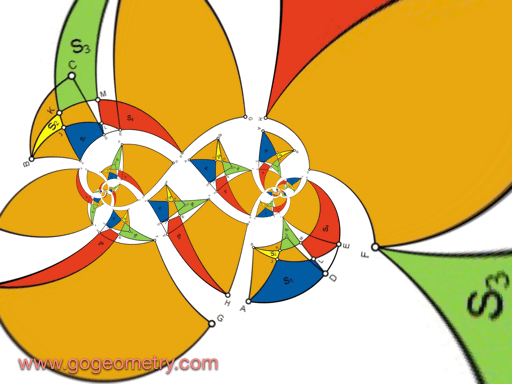
Conformal Mapping

A conformal mapping or conformal transformation is a continuous mapping preserving the form of infinitesimal figures. This conformal map produces a realistic view of the original image or map. This the conformal transformation of problem1426 

See also: Typography and poster of problem 1417.