Geometry Problem 1386: Thabit ibn Qurra (826 -901) Theorem and more conclusions, generalized Pythagorean Theorem to any triangle
Proposition
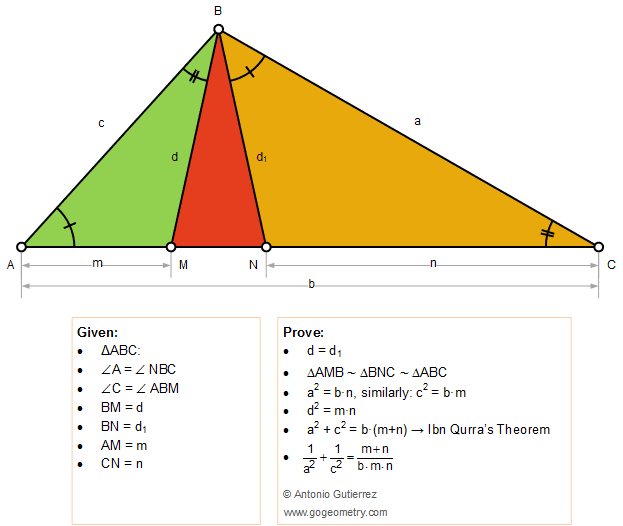
The figure below shows a triangle ABC of sides a, b, c
with the cevians BM and BN so that the angles A and C are congruent to the
angles NBC and ABM, respectively. BM = d, BN = d1, AM = m, and CN = n.
Prove that (1) triangle MBN is isosceles: d = d1; (2) triangles AMB , BNC and ABC are similar; (3) a2
= b.n, similarly c2 = b.m; (4) d2 = m.n; (5) a2 + c2 = b.(m+n) Qurra's
theorem; (6) 1/a2 + 1/c2
= (m+n)/(b.m.n).
| Key Term / Hints | Description |
|---|---|
| Thabit ibn Qurra's Theorem | A generalization of the Pythagorean Theorem to any triangle, involving cevians and angle congruences. |
| Triangle ABC | The primary triangle in the problem with sides a, b, and c. |
| Cevian | A line segment from a vertex to the opposite side of the triangle, intersecting at a point. |
| Isosceles Triangle | A triangle with at least two equal sides. |
| Similarity of Triangles | Triangles that have the same shape but not necessarily the same size, meaning their corresponding angles are equal, and their corresponding sides are proportional. |
| Generalized Pythagorean Theorem | The relationship among the sides of a triangle and cevians, extended from the classical Pythagorean theorem. |
| Proposition Results | Results including the conditions for isosceles triangles, similar triangles, and specific algebraic relationships between sides and cevians. |
Geometric Art: Hyperbolic Kaleidoscope of problem 1386

See also
Conformal Mapping or Transformation of Problem
1386
Flyer of problem 1386 using iPad Apps

Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1381-1390
Visual Index
Open Problems
All Problems
Triangle
Isosceles Triangle
Similarity, Ratios, Proportions
Right Triangle: Pythagoras
View or Post a solution