Proposition

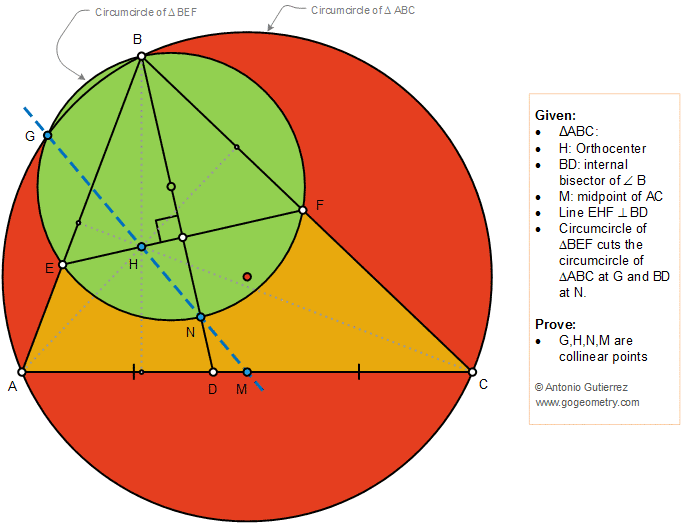
The figure below shows a triangle ABC so that H is the orthocenter, BD is the internal bisector, and M is the midpoint of AC. Line EHF is perpendicular to BD. The circumcircle of the triangle BEF cuts the circumcircle of the triangle ABC and BD at G and N, respectively. Prove that the points G, H, N, and M are collinear.
 

See solution below

See also
Conformal Mapping or Transformation of Problem 1382