Geometry Problem 1323: Discover the Fascinating World of Squares, Angle Trisectors, Diagonals, and Regular Dodecagons with 30-60 Degrees: Unveiling the Secrets of Area!

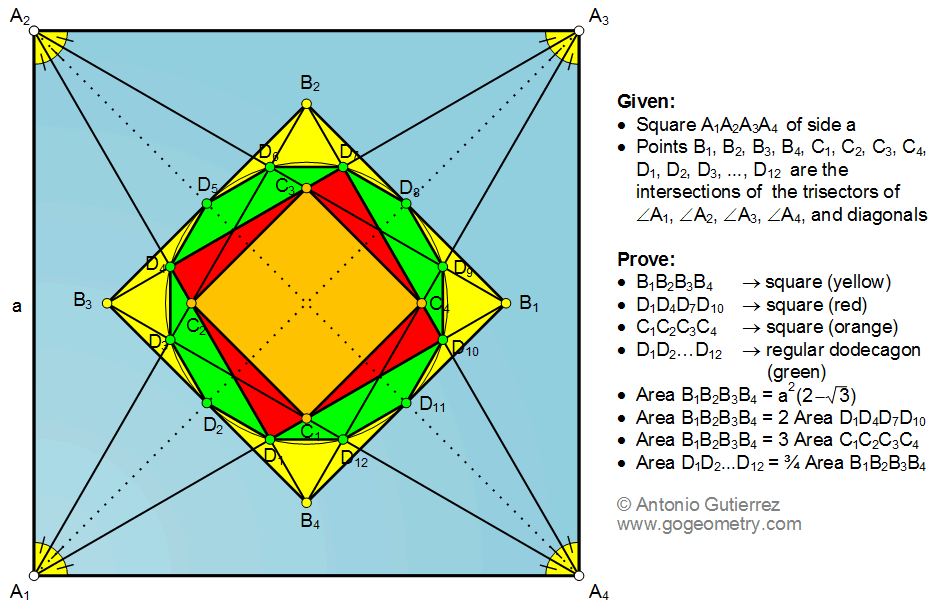
IIn a blue square A₁A₂A₃A₄ with side length 'a', the trisectors of angles A₁, A₂, A₃, A₄ and diagonals intersect at points B₁, B₂, B₃, B₄, C₁, C₂, C₃, C₄, D₁, D₂, D₃, ..., D₁₂ as shown in the figure. We need to prove the following statements: (1) B₁B₂B₃B₄ is a square (yellow); (2) D₁D₄D₇D₁₀ is a square (red); (3) C₁C₂C₃C₄ is a square (orange) ; (4) D₁D₂...D₁₂ is a regular dodecagon (green); (5) Area of B₁B₂B₃B₄ = ; (6) Area of B₁B₂B₃B₄ = 2 times the area of D₁D₄D₇D₁₀; (7) Area B₁B₂B₃B₄ = 3 times the area of C₁C₂C₃C₄; (8) Area D₁D₂...D₁₂ = 3/4 times the area of B₁B₂B₃B₄.
 

Find and share solutions