Geometry Problem 1300: Arbelos, Semicircles, Diameters, Circle, Incircle, Tangent, Perpendicular, Concurrent Lines. Level: School, College, Mathematics Education

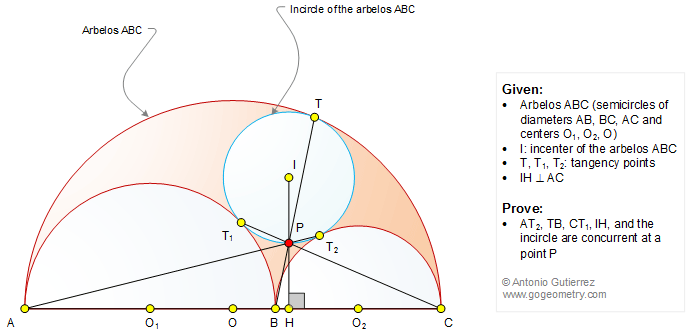
The figure below shows an arbelos ABC (AB, BC, and AC are semicircles of centers O₁, O₂, and O). The incircle I of the arbelos is tangent to semicircles AC, AB, and BC at T, T₁, and T₂, respectively. IH is perpendicular to AC. Prove that AT₂, TB, CT₁, IH, and the incircle are concurrent at a point P.
 
 

See also: Typography of problem 1300 using iPad Apps