Geometry Problem 1249
Elements: Cyclic Quadrilateral, Circle, Triangle, Circumcircle, Angle Bisector, Parallel Lines, Area
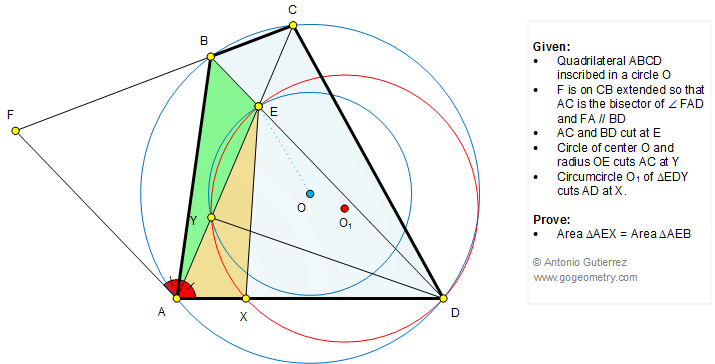
A quadrilateral ABCD is inscribed in a circle O as shown in the
figure below. F is on CB extended so that AC is the bisector of angle FAD
and FA is parallel to BD. AC and BD cut at E. The circle of center O and
radius OE cuts AC at Y. The circumcircle O1 of the triangle EDY cuts
AD at X. Prove that the areas of the triangles AEX and AEB are equal.
This entry contributed by Sumith Peiris, Moratuwa, Sri Lanka.