|
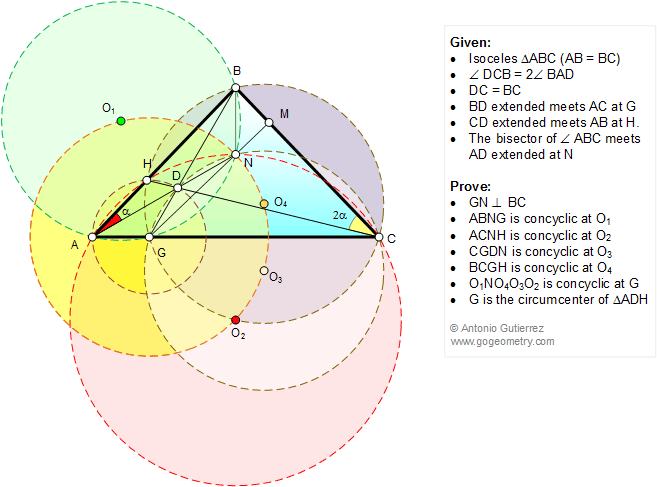
The figure below shows a point D
inside an isosceles triangle ABC (AB = BC) so that
angle DCB = 2 angle BAD and DC = BC. BD extended meets AC at G,
CD extended meets AB at H, and the bisector of angle ABC meets
AD extended at N. Prove that (1) GN is perpendicular to BC at M;
(2) ABNG is concyclic at O1; (3) ACNH is concyclic at O2; (4)
CGDN is concyclic at O3; (5) BCGH is concyclic at O4; (6)
O1NO4O3O2 is concyclic at G; (7) G is the circumcenter of
triangle ADH.
This entry contributed by Sumith Peiris, Moratuwa, Sri Lanka.
See
also:
Geometry art of problem 1163
|