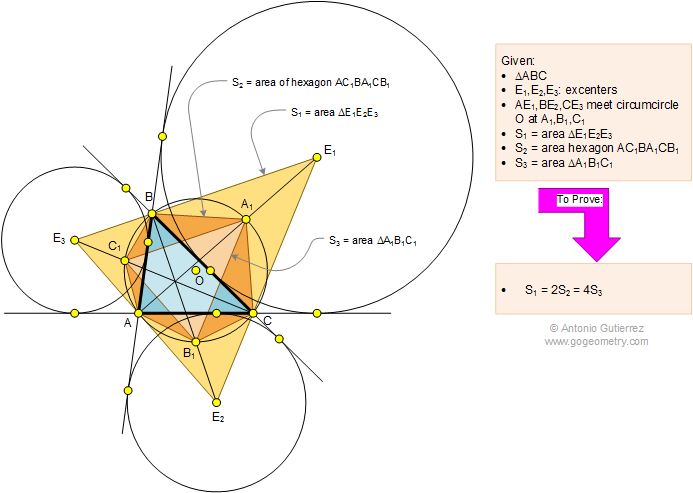
Math: Geometry Problem 1112: Triangle, Excenters, Circumcircle, Circle, Hexagon, Area. Level: High School, College

The figure below shows a triangle ABC with the excenters E₁, E₂, and E₃. Lines AE₁, BE₂, and CE₃ meet circumcircle O at A₁, B₁, and C₁, respectively. If S₁, S₂, and S₃ are the areas of triangle E₁E₂E₃, hexagon AC₁BA₁CC₁, and triangle A₁B₁C₁, respectively, prove that S₁ = 2.S₂ = 4.S₃.
 
 

See also: Kaleidoscope of Problem 1112 base on Poincare Disk Model.