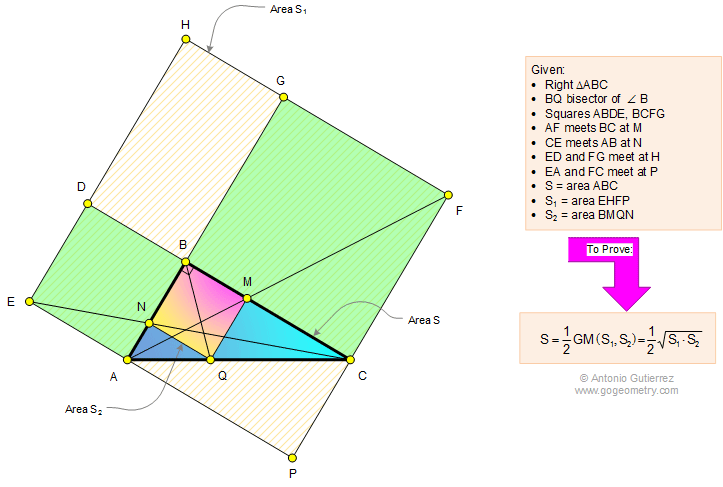
Math: Geometry Problem 1111: Right Triangle, External Squares, Cathetus, Angle Bisector, Area, Geometric Mean. Level: High School, College |
|
Home
|
Geometry
|
Problems |
All Problems
|
Open Problems
|
Visual
Index
|
1111-1120
|
Right Triangle
| Square
|
Triangle &
Squares |
Angle Bisector
|
45 degree |
Triangle area
|
Square area
|
Geometric Mean
|
Email |
Post a comment or solution
|