|
In a triangle, let a line pass through the
orthocenter and intersect the three sides at distinct points.
Reflect this line across each side of the triangle to create
three new lines. Prove that these three reflected lines
intersect at a single point, which lies on the circumcircle of
the triangle.
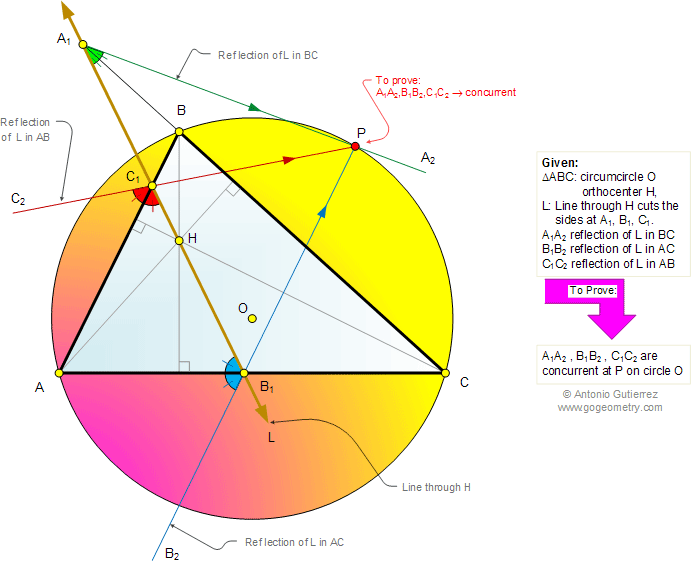
Problem Statement with details
Let ABC be a triangle with orthocenter H.
A line L passing through H intersects sides BC, CA, and AB at points A1, B1, and C1, respectively.
Lines A1A2, B1B2, and C1C2 are the reflections of line L in sides BC, CA, and AB, respectively.
Prove that lines A1A2, B1B2, and C1C2
are concurrent at a point P that lies on the circumcircle of triangle ABC.
Key Concepts:
- Orthocenter: The point where the altitudes of a triangle intersect.
- Reflection: A transformation that flips a figure across a line.
- Concurrency: The property of three or more lines intersecting at a single point.
- Circumcircle: The circle that passes through all three vertices of a triangle.
|