Geometry Problem 295
Archimedean Twin Circles, Arbelos, Semicircles, Harmonic Mean, Radii, Perpendicular

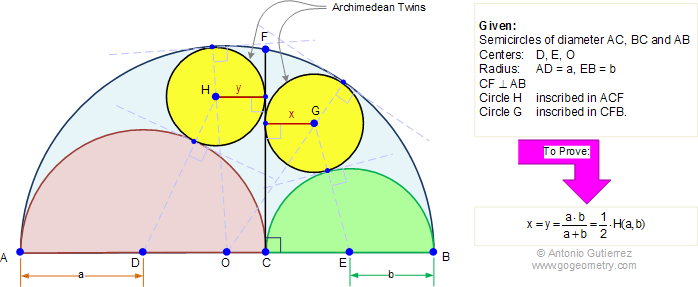
Proposition
The figure shows the semicircles of diameters AB (center O), AC (center D, radius a), and BC (center E, radius b). Prove that radii of circles G (radius x) and H (radius y) inscribed in ACF and CBF, respectively, are equal to one-half the harmonic mean of a and b, that is: \(x=y = \dfrac{a \cdot b}{(a+b)}=\dfrac{1}{2} \cdot H(a,b)\).
The figure included between the circumferences of the three semicircles is "what Archimedes called arbelos."
Geometric Art using iPad or Mobile Apps
Geometric art is a form of art based on the use and application of geometric figures. A geometric figure is any set or combination of points, lines, surfaces and solids.
A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.