Geometry Problem 1605: Triangle, Angle Bisector, and Circumcircle

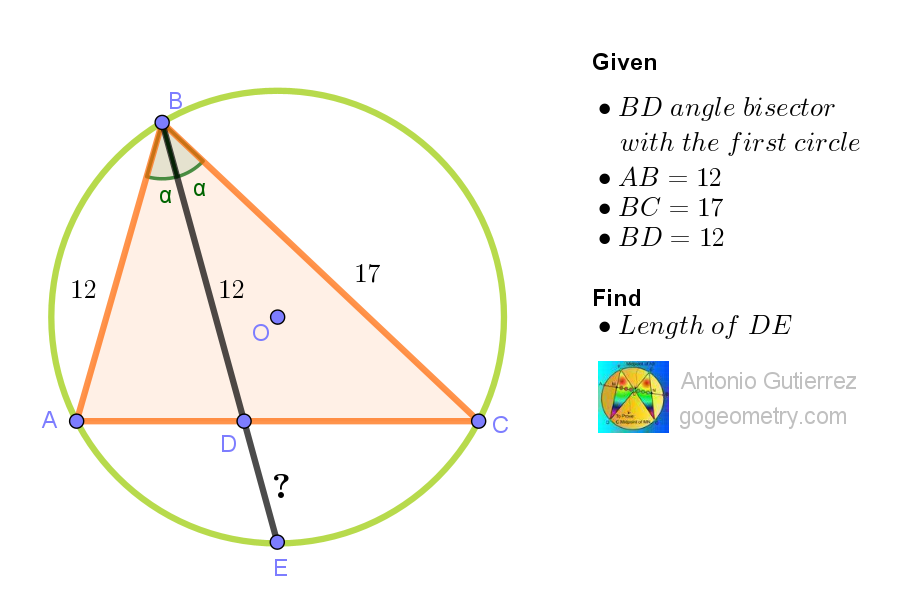
Triangle Problem 1605: Angle Bisector and Circumcircle

In triangle ABC, AB = 12 and BC = 17. The internal angle bisector of ∠ABC intersects AC at point D. Segment BD is extended to meet the circumcircle of triangle ABC at point E. Given that BD = 12, calculate the length of DE.

Suggested Strategies and Key Ideas

  • Explore the Angle Bisector Theorem to relate the segments on side AC.
  • Consider properties of a triangle's circumcircle, especially chords and extended bisectors.
  • Explore Power of a Point or intersecting chords theorems for point B relative to the circle.
  • Use classical geometric relationships and avoid trigonometry whenever possible.
  • Visualize the problem with a clear, scaled diagram to identify potential equalities or similar triangles.
  • Think about angles in the circle: Inscribed, interior angles, equal arcs, and potential isosceles triangles.

🧭 Read more, explore further

Geometry Problems Open Problems Visual Index All Problems Circle Angle Bisector Circumcircle Triangle Isosceles Triangle View or Post a solution