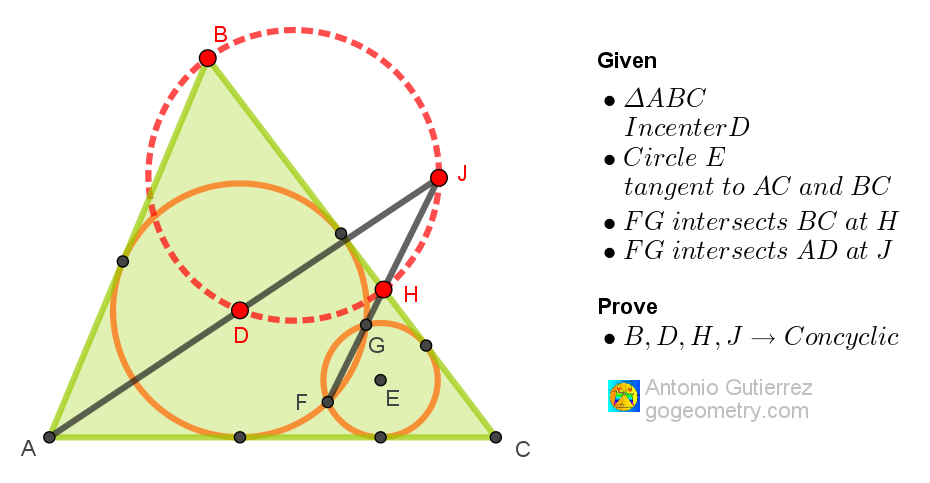
Geometry Problem 1568: Prove Concyclicity of Points B, D , H, J in a Triangle ABC with an Incircle and a Tangent Circle

In a triangle ABC, the incircle centered at D intersects a circle tangent to the sides of angle C at points F and G. The line FG intersects side BC at H and the extension of line AD at J. Prove that points B, D, H, and J are concyclic.

Academic Levels: Suitable for High School and College Mathematics Education

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Term	Description
Triangle ABC	A polygon with three sides and three angles.
Incircle	A circle inscribed in a triangle, touching all three sides.
Center D	The center point of the incircle.
Tangent circle	A circle that touches another circle at exactly one point.
Points F and G	Intersection points of the incircle and the tangent circle.
Line FG	The line segment connecting points F and G.
Point H	Intersection point of line FG and side BC.
Line AD	The line segment connecting points A and D.
Point J	Intersection point of line FG and the extension of line AD.
Concyclic points	Points that lie on the same circle.

---

Flyer of problem 1568 using iPad Apps