Geometry Problem 1495: Unlocking the Mysteries of Circles: Proving the Relationship Between Parallel Chords, 30 degrees and Radius
A circle with radius r has chords AB, CD, and EF parallel to each other,
as well as chords AD and CF parallel to each other. See figure for
visualization. You are required to
prove that \({AB^2+CD^2+EF^2} = {6\cdot r^2}\).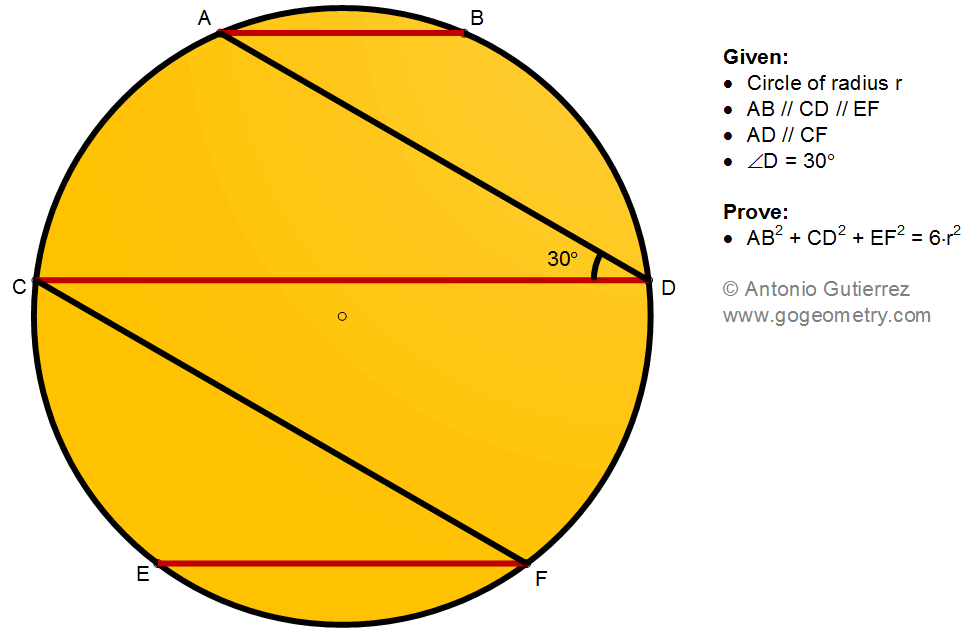
Typography and Sketch: Exploring Problem 1495 with Machu Picchu in the Background

Geometric Art using Mobile Apps
Geometric art is a form of art based on the use and application of geometric figures. A geometric figure is any set or combination of points, lines, surfaces and solids.
A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.
Thematic Poem:
Geometry Problem 1495: Tips and Strategies for Successful Problem Solving
Within a circle, chords do lie,
Parallel to each
other they lie.
AB, CD, and EF, they go,
AD and
CF, they also show.
Radius r is what we know,
But the rest is yet to
show.
To prove a relationship true,
A challenge
lies in front of you.
With angles 30 degrees and more,
And a sum of
squares to explore,
The puzzle seems complex and
deep,
But in geometry, secrets we shall reap.
Look to the figure, visualize,
And let your
reasoning arise.
For in the end, with diligence and
care,
The solution to the mystery will be there.
Unlock the secrets of the circle's lore,
Prove the
relationship once and for all.
With math and wit, we
shall prevail,
And in geometry, our knowledge shall
prevail.
If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.
Recent Additions
Geometry Problems
Open Problems
Visual Index
Ten problems: 1411-1420
All Problems
Circle
Chord
Angle: 30 degrees
Parallel lines
Areas
View or Post a solution
Search our site with Google: