Geometry Problem 1411: Right Triangle, Incircle, Excircle, Tangency Points, Isosceles Right Triangle
Proposition
The figure below shows a right triangle ABC (angle B = 90 degree)
with the incircle I tangent to BC at D. The excircle E corresponding to BC is
tangent to BC and tangent to the extensions of AB and AC at F, G, and H,
respectively. The extensions of GD and FH meet at J. Prove that the
triangle GJH is an isosceles right triangle.
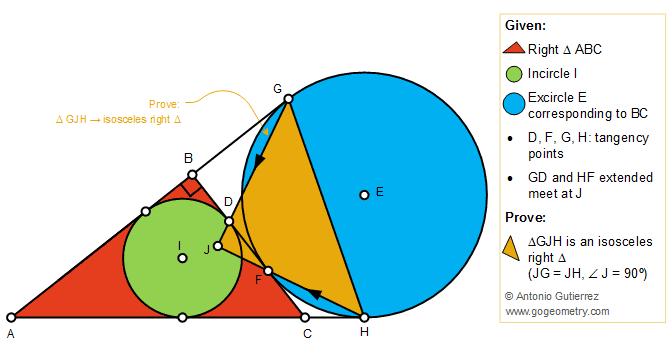
Poster of Problem 1411: Sketching, iPad, Typography, Art
See also: Typography and poster of problem 1408.
Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1411-1420
Visual Index
Open Problems
All Problems
Triangle
Isosceles Triangle
Circle
Incircle
Excircle
Tangent Line
Perpendicular lines
45 degrees
View or Post a solution