Geometry Problem 1401: Right Triangle with three circles on the sides, Isosceles, Diameter, Center, Tangent, Congruence
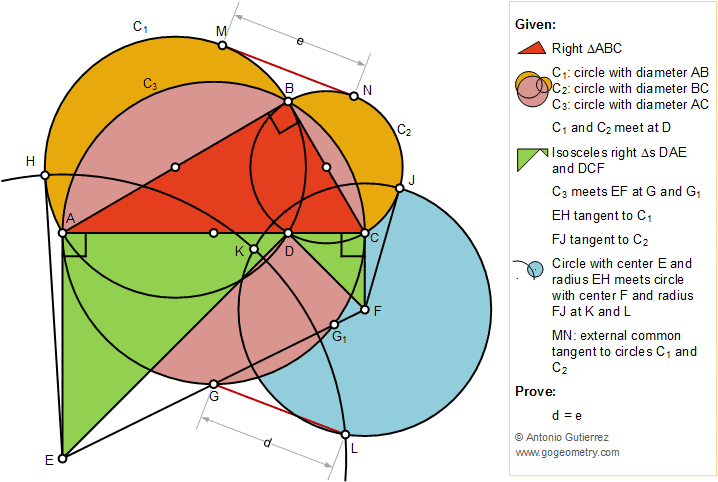
Proposition
The figure below shows
a right triangle ABC with the circles C1, C2, and C3 with diameters AB,
BC, and AC, respectively. C1 and C2 meet at D and DAE and DCF are
isosceles right triangles. C3 meets EF at G and G1. EH is tangent to C1
and FJ is tangent to C2. Circle with center E and radius EH meets the
circle with center F and radius FJ at K and L. If MN is the common external
tangent to C1 and C2, prove that GL = MN.
Sketch of Problem 1401 using iPad Apps

Animation of the Conformal Mapping of Problem 1401
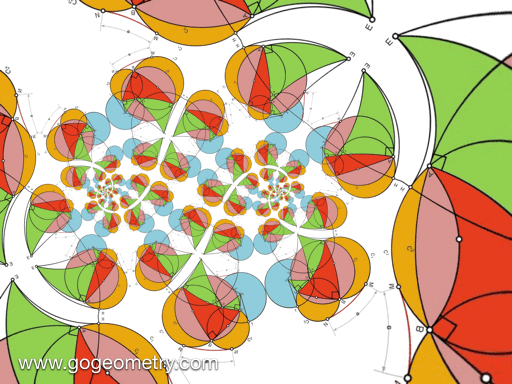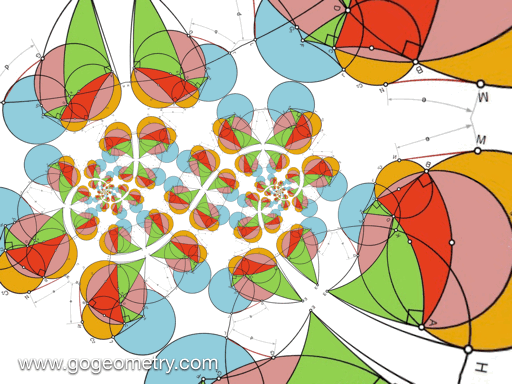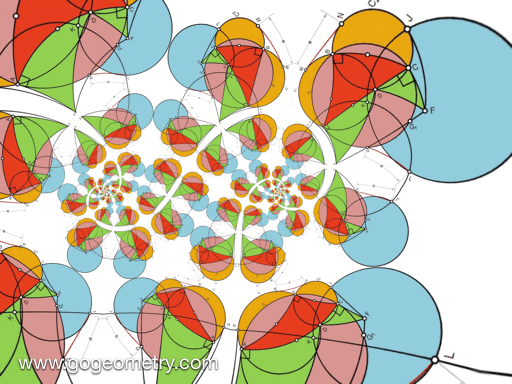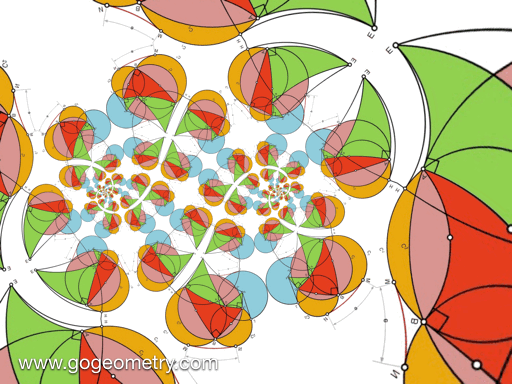
Conformal Mapping
A conformal mapping or conformal transformation is a continuous mapping preserving the form of infinitesimal figures. This conformal map produces a realistic view of the original image or map. This the conformal mapping of problem1401.
Geometric Art using Mobile Apps
Geometric art is a form of art based on the use and application of geometric figures. A geometric figure is any set or combination of points, lines, surfaces and solids. A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.