Geometry Problem 1298
Arbelos, Semicircles, Diameters, Circle, Incircle, Tangent, Angle Bisector, Perpendicular, Midpoint
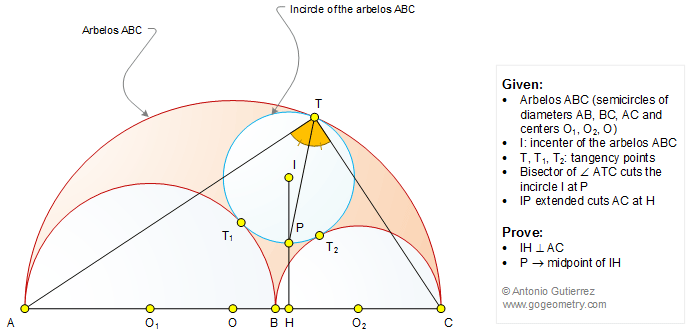
The figure below shows an arbelos ABC (AB, BC, and AC are semicircles of centers O1, O2, and O). The incircle I of the arbelos is tangent to semicircles AC, AB, and BC at T, T1, and T2, respectively. The bisector of the angle ATC cuts the incircle at P and IP extended cuts AC at H. Prove that (1) IH is perpendicular to AC; (2) P is the midpoint of IH.
Mosaic of problem 1298 in Motion using Mobile Apps, iPad
Click on the figure below.
Geometry Problems
1291-1300
Visual Index
Open Problems
All Problems
Arbelos
Triangle
Circle
Semicircle
Tangent Circles
Incircle
Angle Bisector
Angle
Perpendicular lines
Midpoint
Follow our magazine for
daily inspiration straight
to your Flipboard:
View my Flipboard Magazine.