Geometry Problem 1264
Elements: Triangle, Exterior Angle Bisector, Circumcircle, Circle, Perpendicular, 90 Degrees, Concurrent Lines
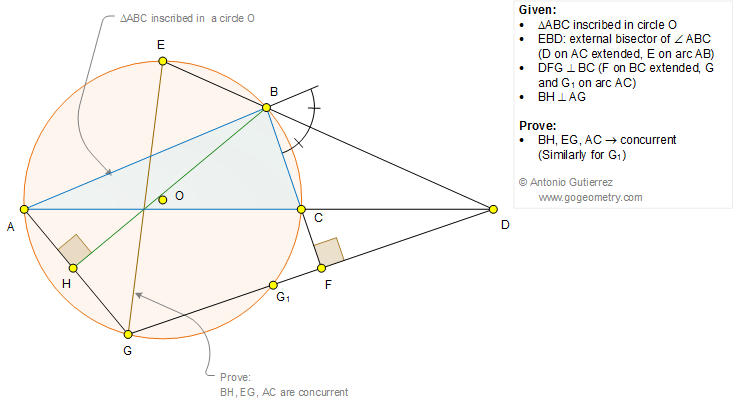
In the figure below, ABC is a triangle inscribed in a circle O. Line EBD is the exterior bisector of the angle ABC (D on AC extended, E on arc AB). Line DFG is perpendicular to BC (F on BC extended, G and G1 on arc AC). If BH is perpendicular to AG, prove that lines BH, EG, and AC are concurrent. Similarly for G1.
Hints, Key Definitions and Descriptions
| Hints, Key Definitions | Description |
|---|---|
| Triangle ABC | A triangle inscribed in circle O. |
| Circle O | The circle in which triangle ABC is inscribed. |
| Line EBD | The exterior bisector of angle ABC, with D on AC extended and E on arc AB. |
| Line DFG | A line perpendicular to BC, with F on BC extended and G and G1 on arc AC. |
| Point H | The point where BH is perpendicular to AG. |
| Lines BH, EG, and AC | Lines that are to be proven concurrent. |
| Inscribed Triangle | A triangle drawn inside a circle such that all its vertices lie on the circle. |
| Angle Bisector | A line segment or ray that divides an angle into two equal angles. |
| External Angle Bisector | A line segment or ray that divides the exterior angle of a triangle into two equal angles. |
| Perpendicular Lines | Two lines that intersect at a right angle (90 degrees). |
| Concurrency of Lines | The property of three or more lines intersecting at a single point. |
Flyer of problem 1264 using iPad Apps

