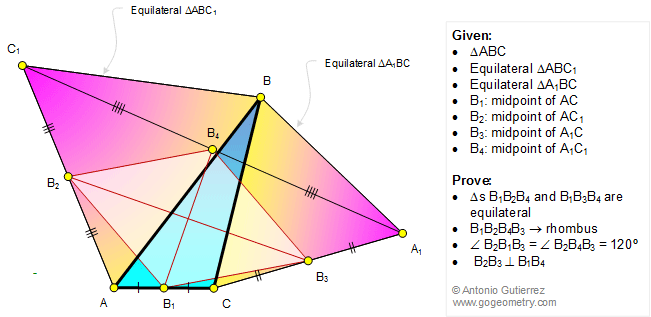
|
In the figure below, equilateral triangles ABC1 and
A1BC are drawn on the sides of a triangle ABC.
If B1, B2, B3, and B4 are the midpoints of AC,
AC1,
A1C, and A1C1, respectively,
prove that (1) triangles B1B2B4
and B1B3B4 are equilateral;
(2) B1B2B4B3
is a rhombus; (3) angle B2B1B3 = angle B2B4B3 = 120
degrees; (4) B2B3 and B1B4
are perpendicular.
|

