Geometry Problem 1139: Triangle, Circumcircle, Angle Bisector, Parallel Lines, 90 Degrees, Concurrent Lines. Level: High School, SAT Prep, Honors Geometry, College, Math Education

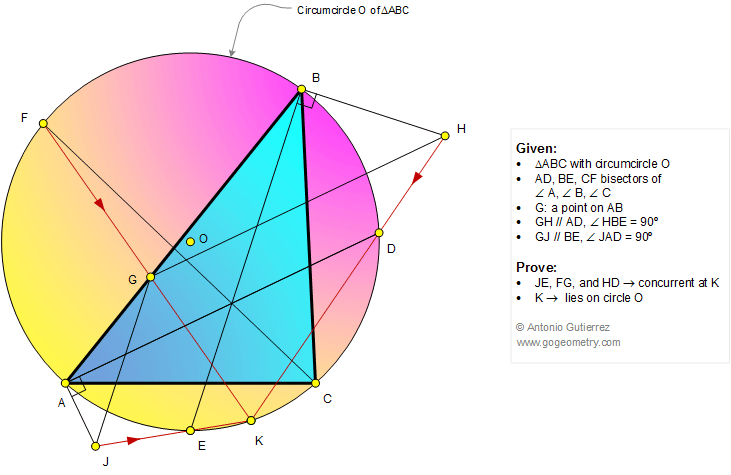
In a triangle ABC (figure below), O is the circumcircle, AD, BE, and CF are bisectors of angle A, B, and C (D,E,F on circle O). G is a point on AB. GH is parallel to AD so that angle HBE = 90 degrees. GJ is parallel to BE so that angle JAD = 90 degrees. Prove that (1) Lines JE, FG, and HD are concurrent at a point K; (2) K lies on circle O.
 

See also:
Triangle
Circle
Circumcircle
Angle Bisector
90 degrees
Parallel lines
Concurrent lines