|
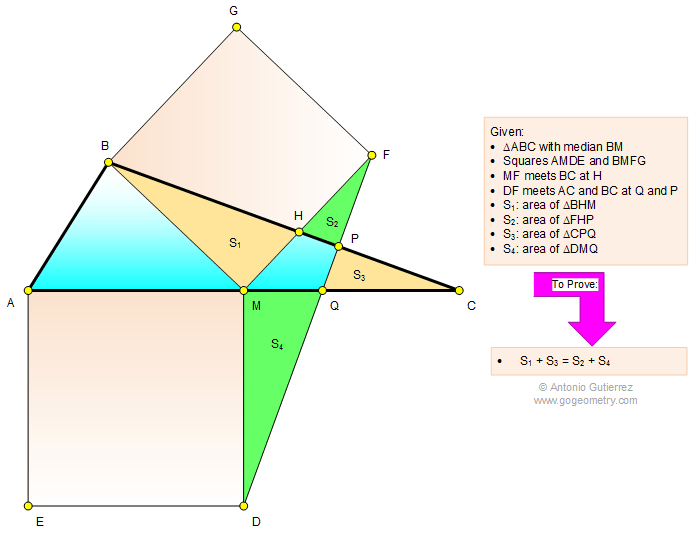
The figure below shows a triangle
ABC with the median BM. AMDE and BMFG are squares so that MF meets
BC at H and DF meets AC and BC at Q and P, respectively. If S1,
S2, S3, and S4 are the areas of
triangles BHM, FHP, CPQ, and DMQ, respectively, prove that S1 +
S3 = S2 + S4.
|