Geometry Problem 1081: Equilateral Triangle, Inscribed Circle, Inradius, Tangent Circles, Radius, Tangent Line, Sangaku Japanese Problem

The figure below shows an equilateral triangle ABC with the inscribed circle of radius r, 3 yellows circles of radius a, 7 green circles of radius b, 6 white circles of radius c and circles C₁ touch each other as shown. Prove that: $(1)\, a = \dfrac{3}{5}r, \,(2)\, b = \dfrac{r}{5}, \,(3)\, c=\dfrac{r}{10}$.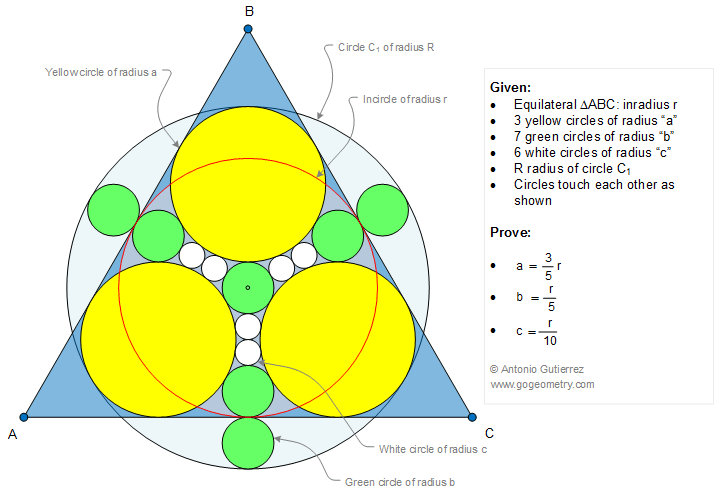

$Equilateral Triangle, Inscribed Circle, Inradius, Tangent Circles, Radius, Tangent Line, Sangaku Japanese Problem$ Reference: Fukagawa Hidetoshi, Tony Rothman, Sacred Mathematics: Japanese Temple Geometry (Princeton University Press, 2008).
See also: Poster and typography of problem 1081.

Recent Additions

Geometry Problems
Open Problems
Visual Index
Ten problems: 1081-1090
All Problems
Equilateral Triangle
Circles
Incircle
Tangent Circles
Tangent Line
Sangaku
View or Post a solution