|
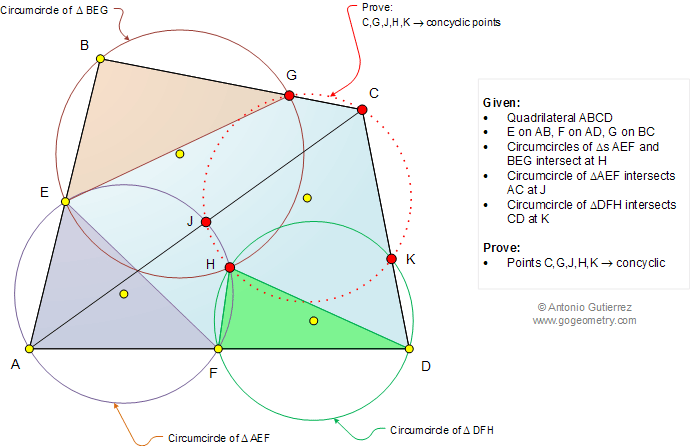
The figure below shows a quadrilateral ABCD
with a point E on AB, F on AD, and G on BC so that the circumcircles of
triangles AEF and BEG intersect at H. The circumcircle of triangle AEF
intersects AC at J and the circumcircle of triangle DFH intersects CD at
K. Prove that C, G, J, H, and K are concyclic points.
|