Geometry Problem 764: Exploring the Relationship Between Triangle, Inradius, Altitudes, and Harmonic Mean - Perfect for High School and College Students!

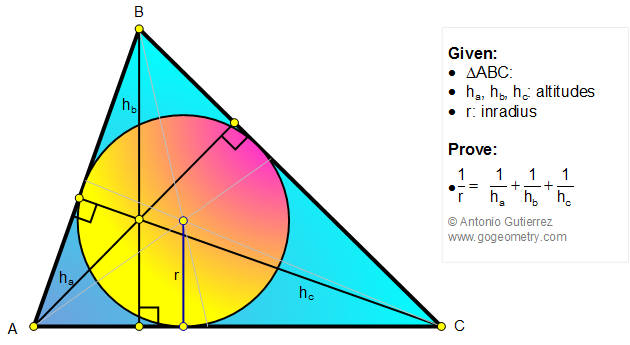
The figure shows a triangle ABC with the inradius r and the altitudes h_a, h_b, h_c. Prove that the inradius is one-third the harmonic mean of the altitudes, therefore, \(\dfrac{1}{r}=\dfrac{1}{h_{a}}+\dfrac{1}{h_{b}}+\dfrac{1}{h_{c}}\)  

Triangle's inradius
One-third harmonic mean of
Heights, beauty revealed.