|
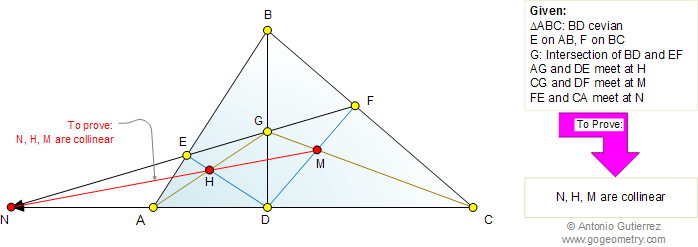
The figure shows a triangle ABC with a
cevian BD. E is a point on AB and F a point on BC. BD
and EF meet at G. AG and DE meet at H, CG and DF meet at M, and FE and
CA meet at N. Prove that points N, H, and M are collinear.
A cevian is a line segment drawn from the vertex of a triangle to the opposite
side (or its extension).
|