Online Geometry Problem 121: Triangle, Median, Similarity and Area. Level: High School, College, Mathematics Education

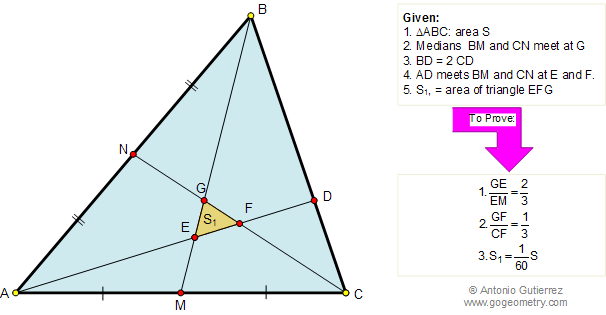
In the figure below, given a triangle ABC of area S, the medians BM and CN meet at G. Let be BD = 2 CD, the cevian AD meets BM and CN at E and F respectively. Area of triangle EFG is S₁. Prove that: GE/EM = 2/3, GF/CF = 1/3 and
S₁ = S/60. View or post a solution.