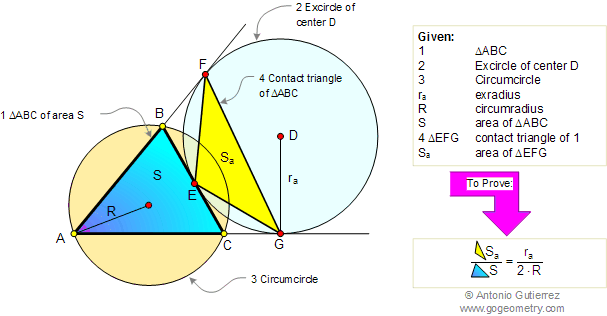
|
Given a triangle ABC of area S, the
excircle of center D, the exradius ra, and the
circumradius R. If Sa is the area of the contact
triangle EFG, from the tangent points of the excircle and
triangle ABC, prove that:
 .
"A great discovery solves a great problem, but there is a grain
of discovery in the solution of any problem. Your problem may be
modest, but if it challenges your curiosity and brings into play
your inventive faculties, and if you solve it by your own means,
you may experience the tension and enjoy the triumph of
discovery. Such expert experiences at a susceptible age may
create a taste for mental work and leave their imprint on mind
and character for a lifetime." George Polya, 1944
HINTS:
1. See Proposed Problems
80,
81,
82.
CONTACT TRIANGLE:
The contact triangle of a triangle
ABC (figure above), also called the intouch triangle, is the
triangle DEF formed by the points of tangency of the incircle of
triangle ABC with triangle ABC.
AREA OF A TRIANGLE:
Semiperimeter and Exradius
Formula
|
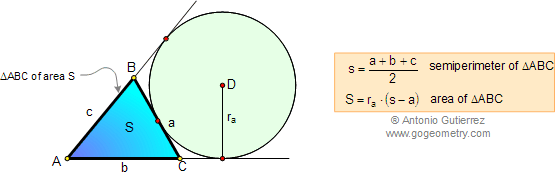
