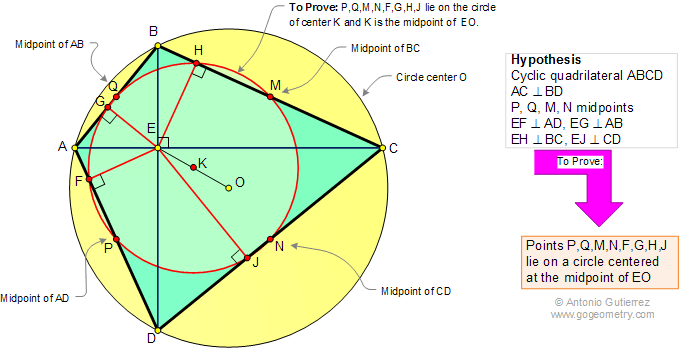
If the diagonals AC and BD of a cyclic quadrilateral ABCD are perpendicular, then the midpoints P, Q, M, N and the feet F, G, H, J of the perpendiculars from the point of intersection of the diagonals to the sides all lie on a circle centered at the midpoint of the line EO.

Brahmagupta (598–668) was an Indian mathematician and astronomer who discovered a neat formula for the area of a cyclic quadrilateral.
 
See also: Brahmagupta's Theorem, Area Formula, Area Formula Extension.